Cho tứ diện SABC có SC=CA=AB=a√2,SC⊥(ABC), tam giác ABC vuông tại A. Các điểm M∈SA,N∈BC sao cho AM=CN=t(0<t<2a)
LG a
Tính độ dài đoạn MN. Tìm giá trị t để MN ngắn nhất.
Lời giải chi tiết:
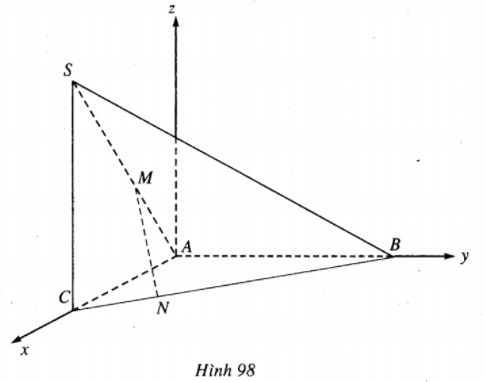
Ta chọn hệ trục Oxyz sao cho gốc tọa độ O trùng A, tia Ox chứa AC, tia Oy chứa AB và tia Oz cùng hướng tới tia CS (h.98). Khi đó, ta có:
A(0;0;0),B(0;a√2;0),C(a√2;0;0),
S(a√2;0;a√2),
M(t√22;0;t√22);N(a√2−t√22;t√22;0)⇒→MN=(√2(a−t);t√22;−t√22)⇒MN=√2(a2−2at+t2)+t22+t22=√3t2−4at+2a2=√3(t−2a3)2+2a23≥a√63.
Dấu "=" xảy ra khi t=2a3 thỏa mãn điều kiện 0 < t < 2a.
Vậy MN ngắn nhất bằng a√63 khi t=2a3.
LG b
Khi đoạn MN ngắn nhất, chứng minh MN là đường vuông góc chung của BC và SA.
Lời giải chi tiết:
Khi MN ngắn nhất thì :
→MN=(a√23;a√23;−a√23)⇒{→MN.→SA=0→MN.→BC=0
⇒MN là đường vuông góc chung của SA và BC.

