Một hình nón có bán kính đáy r, chiều cao bằng 3r. Tìm hình trụ nội tiếp hình nón và thỏa mãn một trong các điều kiện sau :
LG 1
Thể tích của hình trụ đạt giá trị lớn nhất;
Lời giải chi tiết:
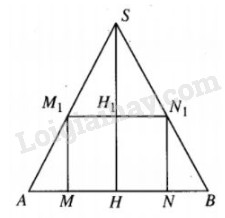
Xét mặt phẳng qua trục hình nón cắt hình nón và hình trụ nội tiếp hình nón, ta được tam giác cân SAB và hình chữ nhật MNN1M1 nội tiếp SAB. Ở đó AB = 2r, SH = 3r, MN bằng đường kính của đáy hình trụ, NN1 bằng chiều cao của hình trụ.
Kí hiệu r1 là bán kính đáy hình trụ, h1 là chiều cao hình trụ, ta có 0<r1<r,0<h1<h và
r1r=SH1SH=SH−h1SH=3r−h13r, từ đó h1=3(r−r1). Khi đó
Thể tích hình trụ là
V=3πr21(r−r1)=3π2r1.r1(2r−2r1).
Từ đó, V đạt giá trị lớn nhất khi và chỉ khi r1=2r3.
LG 2
Diện tích xung quanh của hình trụ đạt giá trị lớn nhất.
Lời giải chi tiết:
Diện tích xung quanh của hình trụ là
S=2πr1.h1=3.2πr1(r−r1)=6πr1(r−r1).
Từ đó S đạt giá trị lớn nhất khi và chỉ khi r1=r2.

