Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng \(4\pi .\)
LG 1
Tính diện tích toàn phần của hình trụ.
Lời giải chi tiết:
Từ \({S_{xq}} = 2\pi R.O{O_1}\) (R là bán kính đáy)
\({S_{xq}} = 2\pi R.(R + O{O_1}),\)
Ta có \({{{S_{tp}}} \over {{S_{xq}}}} = {R \over {O{O_1}}} + 1 = {1 \over 2} + 1 = {3 \over 2}.\)
Vậy \({S_{tp}} = {3 \over 2}.4\pi = 6\pi .\)
LG 2
Tính thể tích khối trụ.
Lời giải chi tiết:
Ta có
\(\eqalign{ & 4\pi = {S_{xq}} = 2\pi R.O{O_1} = 2\pi .R.2R \cr & \Rightarrow R = 1. \cr} \)
Thể tích khối trụ là
\(V = \pi {R^2}.O{O_1} = 2\pi {R^3} = 2\pi .\)
LG 3
Tính thể tích khối lăng trụ n-giác đều nội tiếp hình trụ.
Lời giải chi tiết:
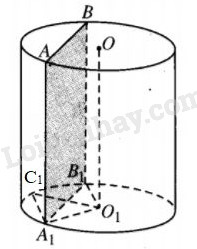
Gọi \({A_1}{C_1}\) là một cạnh của n-giác đều nội tiếp đáy hình trụ thì
\(\widehat {{A_1}{O_1}{C_1}} ={{2\pi } \over n}\) và diện tích đáy hình lăng trụ bằng
\(\eqalign{ & {S_n} = n.{S_{\Delta {A_1}{O_1}{C_1}}} = n.{1 \over 2}{R^2}\sin {{2\pi } \over n} \cr&\;\;\;\;\;\;= {n \over 2}{R^2}\sin {{2\pi } \over n} = {n \over 2}\sin {{2\pi } \over n} \cr & {V_n} = {S_n}.O{O_1} = n\sin {{2\pi } \over n}. \cr} \)
LG 4
Tính thể tích khối cầu ngoại tiếp hình trụ.
Lời giải chi tiết:
Đường tròn lớn của hình cầu ngoại tiếp hình trụ là đường tròn ngoại tiếp thiết diện qua trục. Vậy bán kính mặt cầu là \({R_C} = R\sqrt 2 \) (R là bán kính đáy của hình trụ ). Từ đó thể tích khối cầu phải tìm là
\({V_C} = {4 \over 3}\pi {({R_C})^3} = {{8\pi \sqrt 2 } \over 3}.\)
LG 5
Một mặt phẳng \(\left( \alpha \right)\) song song với trục hình trụ và cắt hình trụ đó theo thiết diện \(AB{B_1}{A_1}\). Biết một cạnh của thiết diện là dây cung của một đường tròn đáy và căng một cung 1200. Tính diện tích thiết diện.
Lời giải chi tiết:
Với thiết diện \(AB{B_1}{A_1}\) như hình vẽ, ta có \(\widehat {{A_1}{O_1}{B_1}}\)=1200, từ đó
\({A_1}{B_1} = 2R\sin {120^0} = R\sqrt 3 .\)
Vậy \({A_1}{B_1} = \sqrt 3 .\)
Do đó diện tích thiết diện là : \({A_1}{B_1}.A{A_1} = \sqrt 3 .2 = 2\sqrt 3 .\)
