Lựa chọn câu để xem lời giải nhanh hơn
Cho khối lăng trụ tam giác đều ABC.A'B'C' có chiều cao bằng h và hai đường thẳng AB' và BC vuông góc với nhau.
LG a
Gọi M' là trung điểm của A'B'. Chứng minh rằng AB′⊥BM′.
Lời giải chi tiết:
(h.109)
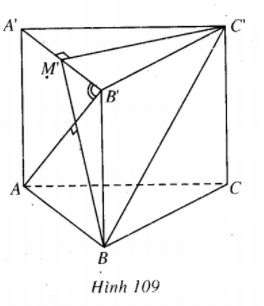
Ta có C'M' ⊥ A'B, C'M' ⊥ AA' => C'M' ⊥ (ABB'A') => C'M' ⊥ AB.
Mặt khác, theo giả thiết BC' ⊥ AB', suy ra AB' ⊥ mp(BC'M').
Do đó AB' ⊥ BM'.
LG b
Tính độ dài đoạn thẳng A'B' theo h.
Lời giải chi tiết:
Từ kết quả của câu a), ta dễ dàng suy ra
ΔBB′M′ đồng dạng ΔB′A′A
⇒A′B′BB′=A′AB′M′⇒A′B′.B′M′=A′A.BB′⇒12A′B′2=h2⇒A′B′=h√2.
LG c
Tính thể tích khối lăng trụ đã cho.
Lời giải chi tiết:
VABC.A′B′C′=SA′B′C′.AA′
=(h√2)2.√34h=√32h3.

