Lựa chọn câu để xem lời giải nhanh hơn
Hãy chứng minh rằng
LG a
Hàm số y=√2x−x2 nghịch biến trên đoạn [1;2]
Lời giải chi tiết:
Hàm số liên tục trên đoạn [1;2] và có đạo hàm
y′=1−x√2x−x2<0 với mọi x∈(1,2)
Do đó hàm số nghịch biến trên đoạn [1;2]
LG b
Hàm số y=√x2−9 đồng biến trên nửa khoảng [3;+∞)
Lời giải chi tiết:
Hàm số liên tục trên nửa khoảng [3;+∞) và có đạo hàm
y′=x√x2−9>0 với mọi x∈(3,+∞)
Do đó hàm dố đồng biến tên nửa khoảng [3;+∞)
LG c
Hàm số y=x+4x nghịch biến trên mỗi nửa khoảng [-2;0) và (0;2]
Lời giải chi tiết:
TXĐ: x≠0
y′=1−4x2
y′=0⇔x=±2
BBT
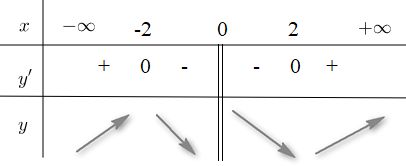
Từ BBT ta có hàm số y=x+4x nghịch biến trên mỗi nửa khoảng [-2;0) và (0;2]

