Chứng minh rằng:
LG a
Hai hình hộp chữ nhật bằng nhau nếu các kích thước của chúng bằng nhau.
Lời giải chi tiết:
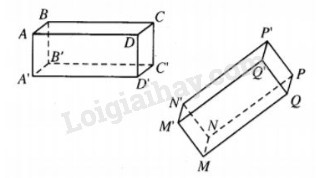
Giả sử hai hình hộp chữ nhật ABCD.A′B′C′D′ và MNPQ.M′N′P′Q′ có AB=MN,AD=MQ, AA′=MM′
Ta thấy rằng khi đó, hai tứ diện ABDA’ và MNQM’ có các cạnh tương ứng bằng nhau nên có phép dời hình f biến A, B, D, A’ lần lượt thành các điểm M,N,Q,M’.
Khi đó vì f biến tam giác ABD thành tam giác MNQ nên f biến điểm C thành điểm P. Cũng tương tự như thế, f biến B’ thành N’, biến D’ thành Q’ và biến C’ thành P’.
Vậy f biến hình hộp chữ nhật thứ nhất thành hình hộp thứ hai do đó hai hình hộp bằng nhau.
LG b
Hai hình lập phương bằng nhau nếu các đường chéo của chúng có độ dài bằng nhau.
Lời giải chi tiết:
Hiển nhiên đường chéo của hai hình lập phương bằng nhau khi và chỉ khi cạnh của chúng bằng nhau, do đó theo a), hai hình lập phương đó bằng nhau.

