Đề bài
Với các giá trị nào của m, hàm số
\(y = x + 2 + {m \over {x - 1}}\)
Đồng biến trên mỗi khoảng xác định của nó ?
Lời giải chi tiết
Ta có \(y' = 1 - {m \over {{{(x - 1)}^2}}}\) với mọi \(x \ne 1\)
+) Nếu \(m \le 0\) thì y’ > 0 với mọi \(x \ne 1\) . Do đó hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
+) Nếu m > 0 thì
\(y' = {{{x^2} - 2x + 1 - m} \over {{{(x - 1)}^2}}}\)
\(y' = 0 \Leftrightarrow {x^2} - 2x + 1 - m = 0\) \( \Leftrightarrow x = 1 \pm \sqrt m \)
Bảng biến thiên
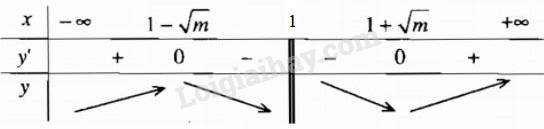
Hàm số nghịch biến trên mỗi khoảng \(\left( {1 - \sqrt m ;1} \right)\) và \(\left( {1;1 + \sqrt m } \right)\).
Điều kiện đòi hỏi không được thỏa mãn.
Vậy hàm số đồng biến trên mỗi khoảng xác định của nó khi và chỉ khi \(m \le 0\).

