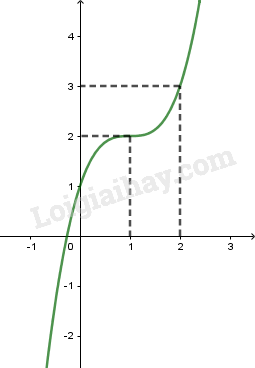
Cho hàm số
y=x3−3mx2+(2m−1)x+1
LG a
Chứng minh rằng với mọi giá trị của m, đồ thị (Cm) của hàm số đã cho và đường thẳng y=2mx−4m+3 luôn có một điểm chung cố định.
Lời giải chi tiết:
Đường thẳng y=2m(x−2)+3 luôn đi qua điểm cố định A(2;3)
Vì f(2)=23−3m.22+3(2m−1).2+1=3 với mọi m nên điểm A thuộc (Cm) với mọi m.
LG b
Tìm giá trị của m sao cho đường thẳng đã cho và đường cong (C) cắt nhau tại ba điểm phân biệt.
Lời giải chi tiết:
Hoành độ giao điểm của đường thẳng và đường cong (Cm) là nghiệm của phương trình:
x3−3mx2+3(2m−1)x+1=2m(x−2)+3
⇔x3−3mx2+3(2m−1)x−2−2m(x−2)=0⇔(x−2)[x2−(3m−2)x+1−2m]=0
Để đường thẳng đã cho cắt (C) tại 3 điểm phân biệt thì x2−(3m−2)x+1−2m=0 có hai nghiệm phân biệt khác 2
⇔{Δ=(3m−2)2−4(1−2m)>022−(3m−2).2+1−2m≠0⇔{9m2−4m>0−8m+9≠0⇔{m>49,m<0m≠98
Vậy m<0 hoặc m>49 và m≠98
LG c
Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 1.
Lời giải chi tiết:
Với m=1 ta có: y=x3−3x2+3x+1
+) TXĐ: D=R
+) Chiều biến thiên:
limx→+∞y=+∞,limx→−∞y=−∞
y′=3x2−6x+3 =3(x−1)2≥0,∀x∈R
Hàm số đồng biến trên R và không có cực trị.
BBT:
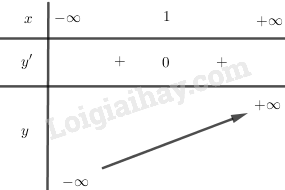
+) Đồ thị: