Đề bài
Với giá trị nào của m, phương trình
4x3−3x−2m+3=0
Có một nghiệm duy nhất ?
Phương pháp giải - Xem chi tiết
Phương trình đã cho tương đương với phương trình
f(x)=4x3−3x+3=2m
Do đó nghiệm của phương trình đã cho là hoành độ giao điểm của đồ thị (C) của hàm số y=4x3−3x+3 và đường thẳng y=2m
Lập bảng biến thiên của hàm số y=4x3−3x+3.
Từ đó dễ dàng tìm được các giá trị sao cho đường thẳng y=2m cắt (C) tại đúng một điểm.
Lời giải chi tiết
Ta có:
4x3−3x−2m+3=0⇔4x3−3x+3=2m
Xét hàm f(x)=4x3−3x+3 trên R ta có:
y′=12x2−3y′=0⇔12x2−3=0⇔x2=14⇔x=±12
BBT:
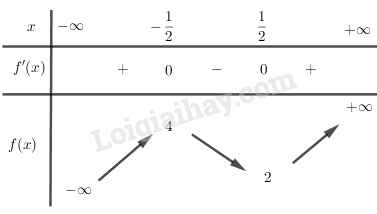
Để phương trình có nghiệm duy nhất thì đường thẳng y=2m cắt đồ thị hàm số y=f(x) tại 1 điểm duy nhất.
Quan sát BBT ta thấy [2m<22m>4⇔[m<1m>2
Vậy m<1 hoặc m>2.

