Tìm các đường tiệm cận của đồ thị các hàm số sau
LG a
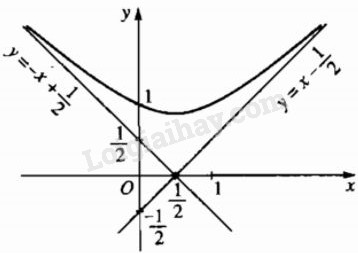
y=√x2−x+1
Lời giải chi tiết:
Ta có :
a=limx→+∞yx=limx→+∞√x2−x+1x
=limx→+∞x√1−1x+1x2x
=limx→+∞√1−1x+1x2=1
b=limx→+∞(y−x)=limx→+∞(√x2−x+1−x)=limx→+∞−x+1√x2−x+1+x=limx→+∞−1+1x√1−1x+1x2+1=−12
Đường thẳng y=x−12 là tiệm cận xiên của đồ thị (khi x→+∞)
a=limx→−∞yx=limx→−∞√x2−x+1x=limx→−∞−x√1−1x+1x2x=limx→−∞(√1−1x+1x2)=−1
b=limx→−∞(y+x)=limx→−∞(√x2−x+1+x)=limx→−∞−x+1√x2−x+1−x=limx→−∞−x+1−x√1−1x+1x2−x=limx→−∞−1+1x−√1−1x+1x2−1=12
Đường thẳng y=−x+12 là tiệm cận xiên của đồ thị (khi x→−∞)
LG b
y=x+√x2+2x
Lời giải chi tiết:
a=limx→+∞yx=limx→+∞x+√x2+2xx=limx→+∞(1+√1+2x)=2b=limx→+∞(y−2x)=limx→+∞(x+√x2+2x−2x)=limx→+∞(√x2+2x−x)=limx→+∞2x√x2+2x+x=limx→+∞2√1+2x+1=1⇒a=2,b=1
Tiệm cận xiên: y = 2x + 1 (khi x→+∞)
limx→−∞(x+√x2+2x)=limx→−∞−2xx−√x2+2x=limx→−∞−2xx−|x|√1+2x=limx→−∞−2xx+x√1+2x=limx→−∞−21+√1+2x=−1
Tiệm cận ngang: y = -1 (khi x→−∞)
LG c
y=√x2+3
Lời giải chi tiết:
a=limx→+∞yx=limx→+∞√x2+3x=limx→+∞√1+3x21=1b=limx→+∞(y−x)=limx→+∞(√x2+3−x)=limx→+∞3√x2+3+x=0⇒a=1,b=0
Tiệm cận xiên: y = x (khi x→+∞)
a=limx→−∞yx=limx→−∞√x2+3x=limx→−∞|x|√1+3x2x=limx→−∞−x√1+3x2x=limx→−∞(−√1+3x2)=−1b=limx→−∞(y+x)=limx→−∞(√x2+3+x)=limx→−∞3√x2+3−x=0⇒a=−1,b=0
Tiệm cận xiên: y = -x (khi x→−∞)
LG d
y=x+2√x
Lời giải chi tiết:
limx→0+y=limx→0+(x+2√x)=+∞
Tiệm cận đứng: x = 0 (khi x→0+)
limx→+∞(y−x)=limx→+∞2√x=0
Tiệm cận xiên: y = x (khi x→+∞)

