Xét hình lăng trụ tam giác đều với chiều cao h, nội tiếp một mặt cầu bán kính R (h < 2R) (tức sáu đỉnh của hình lăng trụ nằm trên mặt cầu đó).
LG a
Tính cạnh đáy của hình lăng trụ.
Lời giải chi tiết:
(h.107).
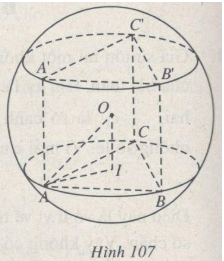
Gọi O là tâm của mặt cầu ngoại tiếp hình lăng trụ, I là hình chiếu của O trên mặt phẳng (ABC). Khi đó ta có : OA=OB=OC=R,OI=12h. Tam giác OAI vuông tại I nênAI2=OA2−OI2=R2−h24.
IA là bán kính đường tròn ngoại tiếp tam giác đều ABC nên
AB=IA√3=√3(R2−h24).
Vậy cạnh đáy của hình lăng trụ bằng
12√3(4R2−h2).
LG b
Tính thể tích của khối lăng trụ.
Lời giải chi tiết:
Thể tích của khối lăng trụ ABC.A'B'C' là :
V=SABC.h=AB2√34h=3√316(4R2−h2)h.
LG c
Tính h theo R để mỗi mặt bên của hình lăng trụ là hình vuông.
Lời giải chi tiết:
Mỗi mặt bên của hình lăng trụ là hình vuông khi và chỉ khi AB = h, tức 12√3(4R2−h2)=h⇔h=√127R (để ý rằng √127< 2).

