Đề bài
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z sao cho \({{z - 2} \over {z + 2}}\) có một acgumen bằng \({\pi \over 3}\)
Lời giải chi tiết
\({{z - 2} \over {z + 2}} = {{z\overline z - 4 + 2\left( {z - \overline z} \right)} \over {{{\left| {z + 2} \right|}^2}}}\) có một acgumen bằng \({\pi \over 3}\) khi và chỉ khi \(z\bar z - 4 + 2\left( {z - \bar z} \right) = l\left( {1 + i\sqrt 3 } \right)\), l là số thực dương.
Nếu viết \(z = x + yi\left( {x,y \in R} \right)\) thì
\(\eqalign{& z\bar z - 4 + 2\left( {z - \bar z} \right) = {x^2} + {y^2} - 4 + 4yi \cr&\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\; = l + l\sqrt 3 i\left( { > 0} \right) \cr& \Leftrightarrow 4y = \left( {{x^2} + {y^2} - 4} \right)\sqrt 3 \cr&\Leftrightarrow {x^2} + {\left( {y - {2 \over {\sqrt 3 }}} \right)^2} - {{16} \over 3} = 0 \cr} \)
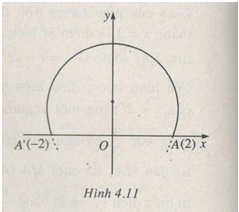
Vậy M chạy trên cung tròn có tâm biểu diễn \({2 \over {\sqrt 3 }}i\) và có bán kính bằng \({4 \over {\sqrt 3 }}\) nằm ở phía trên trục thực.
Chú ý: A’, A là các điểm theo thứ tự biểu diễn -2. 2 thì điều kiện \({{z - 2} \over {z + 2}}\) có một acgumen bằng \({\pi \over 3}\) có nghĩa là góc lượng giác tia đầu MA’, tia cuối MA’ (M là điểm biểu diễn z) bằng \({\pi \over 3}\). Suy ra quỹ tích của M là cung tròn chứa góc \({\pi \over 3}\) căng trên đoạn A’A (không kể A, A’) (h.4.11)