Đề bài
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = b; cạnh bên SA vuông góc với mặt phẳng đáy, AS = 2a. Gọi M là điểm bất kì trên cạnh AS, đặt \(AM = x\left( {0 \le x \le 2{\rm{a}}} \right)\).
a) Thiết diện của hình chóp S.ABCD khi cắt bởi mp(MBC) là hình gì? Tính diện tích thiết diện.
b) Tính khoảng cách từ điểm S đến mp(MBC) ứng với mỗi vị trí của M.
Lời giải chi tiết
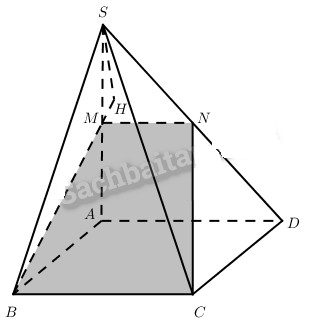
a) Vì \(BC//SA{\rm{D}},M \in mp\left( {SA{\rm{D}}} \right) \cap mp\left( {MBC} \right)\)
nên \(mp\left( {MBC} \right) \cap \left( {SA{\rm{D}}} \right) = MN\)
mà \(MN//BC\left( {N \in S{\rm{D}}} \right)\).
Như vậy BMNC là hình thang.
Mặt khác \(BC \bot \left( {SAB} \right)\) nên \(BC \bot BM\).
Vậy BMNC là hình thang vuông.
Do đó thiết diện của hình chóp S.ABCD khi cắt bởi mp(MBC) nói chung là hình thang vuông.
Khi x = 0 thì thiết diện là hình chữ nhật ABCD, và khi x = 2a thì thiết diện là tam giác SBC.
Ta có
\(\eqalign{ & {S_{BMNC}} = {1 \over 2}\left( {BC + MN} \right).BM \cr & B{M^2} = {a^2} + {x^2} \cr} \)
hay \(BM = \sqrt {{a^2} + {x^2}} \)
\({{MN} \over {A{\rm{D}}}} = {{SM} \over {SA}} = {{2{\rm{a}} - x} \over {2{\rm{a}}}}\), từ đó \(MN = b.{{2{\rm{a}} - x} \over {2{\rm{a}}}}\).
Từ đó
\(\eqalign{ & {S_{BMNC}} = {1 \over 2}\left( {b + b.{{2{\rm{a}} - x} \over {2{\rm{a}}}}} \right).\sqrt {{a^2} + {x^2}} \cr & = {b \over {4{\rm{a}}}}\left( {4{\rm{a}} - x} \right)\sqrt {{a^2} + {x^2}} \cr} \)
b) Do \(\left( {BMNC} \right) \bot \left( {SAB} \right)\) nên khi kẻ SH vuông góc với đường thẳng \(BM\left( {H \in BM} \right)\) thì \(SH \bot \left( {BMNC} \right)\).
Khoảng cách từ S đến mp(BCM) là SH. Dễ thấy
\(SH.BM = 2{{\rm{S}}_{SBM}} = 2.{1 \over 2}a\left( {2{\rm{a}} - x} \right)\)
Vậy \(SH = {{a\left( {2{\rm{a}} - x} \right)} \over {\sqrt {{a^2} + {x^2}} }}\)

