Đề bài
Cho hai nửa mặt phẳng (P) và (Q) vuông góc với nhau theo giao tuyến ∆. Trên ∆ lấy hai điểm A, B cố định với AB=a√2 (a là độ dài cho trước). Trên nửa đường thẳng Ax vuông góc với ∆ và ở trong (P) lấy điểm M khác A. Đặt AM = m. Trên nửa đường thẳng By vuông góc với ∆ và trong (Q) lấy điểm N sao cho BN=a2m.
a) Chứng minh các mặt của tứ diện ABMN là các tam giác vuông.
b) Với giá trị nào của m thì MN có độ dài bé nhất? Tính giá trị đó.
c) Chứng minh rằng chân mỗi đường cao của tứ diện đó xuất phát từ A và B nằm trên đường tròn cố định khi M thay đổi.
Lời giải chi tiết
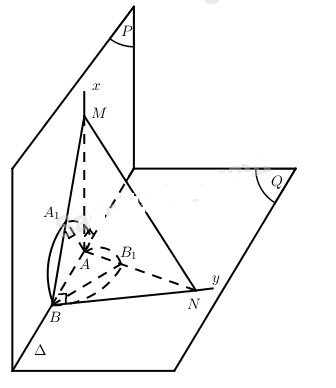
a) Vì (P)⊥(Q),(P)∩(Q)=AB,
M∈(P),MA⊥AB nên MA⊥(Q). Do đó MAB, MAN là các tam giác vuông tại A.
Tương tự như trên, các tam giác MBN, ABN vuông tại B.
b) Vì
MN2=MA2+AB2+BN2=m2+2a2+a4m2
Từ đó MN có độ dài bé nhất khi và chỉ khi m2+a4m2 bé nhất.
Mặt khác m2.a4m2=a4.
Vậy MN có độ dài bé nhất khi và chỉ khi:
m2=a4m2⇔m=a.
c) Vì (MAB)⊥(NMB) nên khi kẻ AA1 vuông góc với BM tại A1 thì AA1⊥(BMN), tức A1 là chân đường cao của tứ diện ABMN kẻ từ đỉnh A.
Như vậy A1 thuộc (P) và ^BA1A=900, từ đó A1 thuộc đường tròn đường kính AB trong (P). Đường tròn này cố định.
Tương tự như trên, chân đường cao B1 kẻ từ đỉnh B của tứ diện ABMN cũng thuộc đường tròn đường kính AB nằm trong mặt phẳng (Q).

