Đề bài
Cho tứ diện ABCD có \(C{\rm{D}} = {4 \over 3}AB\). Gọi I, J, K lần lượt là trung điểm của BC, AC, BD. Cho biết \(JK = {5 \over 6}AB\), tính góc giữa đường thẳng CD với các đường thẳng IJ và AB.
Lời giải chi tiết
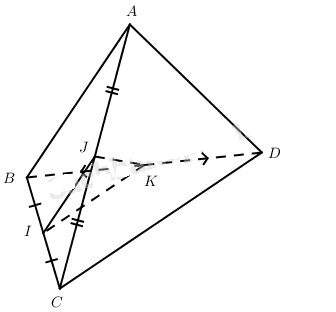
Ta có:
\(\eqalign{ & IJ = {1 \over 2}AB \cr & IK = {1 \over 2}CD = {2 \over 3}AB \cr & I{J^2} + I{K^2} = {1 \over 4}A{B^2} + {4 \over 9}A{B^2} \cr & = {{25} \over {36}}A{B^2} \cr} \)
mà \(I{K^2} = {{25} \over {36}}A{B^2}\) nên \(I{J^2} + I{K^2} = J{K^2}\)
Vậy \(JI \bot IK\) .
Do IJ // AB, IK // CD nên góc giữa AB và CD bằng 90°
Mặt khác IJ // AB mà AB ⊥ CD nên IJ ⊥ CD
Vậy góc giữa IJ và CD bằng 90°.

