Đề bài
Cho hình bình hành ABCD. Qua đỉnh A, B, C, D dựng các đường thẳng a, b, c, d tương ứng song song với nhau và không thuộc mp(ABCD). Trên mỗi đường thẳng a, b, c, d lần lượt lấy các điểm A1,B1,C1,D1. Chứng minh rằng:
a) Nếu các điểm A1,B1,C1,D1 không đồng phẳng thì đường thẳng nối trung điểm A1C1 và trung điểm B1D1 luôn đi qua một điểm cố định.
b) Bốn điểm A1,B1,C1,D1 đồng phẳng khi và chỉ khi trung điểm của A1C1 trùng với trung điểm B1D1.
c) Nếu bốn đường thẳng AC1,BD1,CA1,DB1 đôi một cắt nhau thì ABCD.A1B1C1D1 là một hình hộp.
Lời giải chi tiết
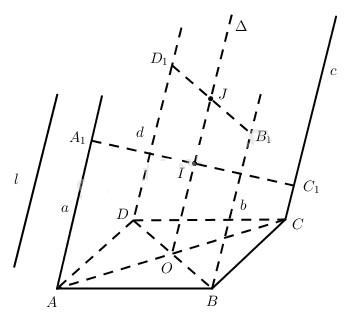
a) Xét phép chiếu song song lên mp(ABCD) theo phương chiếu l // a. Khi đó A1C1 có hình chiếu là AC nên trung điểm I của A1C1 có hình chiếu là trung điểm O của AC.
Tương tự, trung điểm J của B1D1 có hình chiếu là trung điểm O của BD.
Do đó, ba điểm I, J, O phải nằm trên một đường thẳng ∆. Đường thẳng ∆ này đi qua điểm cố định O.
b) Nếu A1,B1,C1,D1 đồng phẳng thì A1B1//C1D1 vì chúng là giao tuyến của mp(A1B1C1D1) với hai mặt phẳng song song (ABB1A1),(DCC1D1).
Tương tự, ta có A1D1//B1C1. Vậy tứ giác A1B1C1D1 là một hình bình hành. Do đó trung điểm I của A1C1 trùng với trung điểm J của B1D1.
● Ngược lại, nếu I trùng với J thì các điểm A1,B1,C1,D1 cùng nằm trên mặt phẳng xác định bởi hai đường thẳng cắt nhau A1C1 và B1D1.
c)
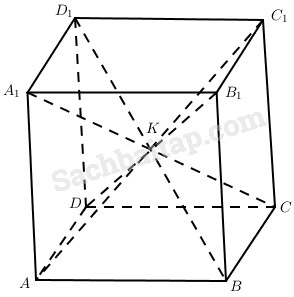
Giả sử AC1 cắt BD1 tại K. Khi đó, ta có mp(AC1,BD1)≡mp(ABC1D1).
Mặt phẳng này cắt hai mặt phẳng song song (ABB1A1),(DCC1D1) theo hai giao tuyến song song AB và C1D1, suy ra C1D1//CD. Mặt khác DD1//CC1.
Vậy tứ giác CDD1C1 là hình bình hành.
Do đó: CD=C1D1⇒C1D1=BA.
Như vậy ABC1D1 là hình bình hành và K là trung điểm của AC1 và BD1.
Tương tự, nếu BD1 cắt CA1 tại K’ thì BCD1A1 là hình bình hành và K’ là trung điểm của BD1 và CA1 nên K’ ≡ K.
Tương tự, ta cũng suy ra K là trung điểm của B1D, các mặt ABB1A1,BCC1B1 đều là hình bình hành và từ đó A1B1C1D1 cũng là hình bình hành. Vậy ABCD.A1B1C1D1 là hình hộp.

