Đề bài
Cho M và N lần lượt là trung điểm của các cạnh AB, A1D1 của hình hộp ABCD.A1B1C1D1.
a) Xác định giao điểm P và Q của mặt phẳng (CMN) với các đường thẳng B1C1 và DB1.
b) Hãy biểu thị các vectơ →AP,→AQ qua các vectơ →a,→b,→c trong đó →b=→AB,→c=→AD,→a=→AA1.
Lời giải chi tiết
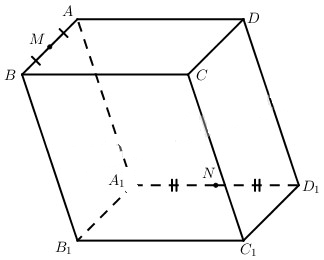
a) Đặt →AA1=→a,→AB=→b,→AD=→c.
P là giao điểm của mp(CMN) với đường thẳng B1C1 khi và chỉ khi C, M, N, P thuộc một mặt phẳng và P thuộc đường thẳng B1C1.
Ta có các điểm M, N, C, P thuộc một mặt phẳng nên tồn tại các số x, y, z sao cho:
x+y+z=1(∗)
và →AP=x→AM+y→AN+z→AC.
Ta có:
→AP=x.→b2+y(→a+→c2)+z(→b+→c)=y→a+(x2+z)→b+(y2+z)→c(1)
Vì P thuộc đường thẳng B1C1 nên →B1P=t→B1C1, từ đó →AP=→b+→a+t→c(2)
Từ (1), (2) và do →a,→b,→c không đồng phẳng nên
{y=1x2+z=1y2+z=t(∗∗)
Kết hợp (*) và (**), ta có:
{y=1x2+z=1y2+z=tx+y+z=1⇒z=−x⇒x2−x=1⇔x=−2⇒z=2,t=52
Vậy giao điểm của mp(CMN) với đường thẳng B1C1 là điểm P xác định bời
→B1P=52→B1C1 .
Tương tự như trên, nếu gọi Q là giao điểm của mp(CMN) với đường thẳng B1D thì ta có x+y+z=1.
và
→AQ=x→AM+y→AN+z→AC=y→a+(x2+z)→b+(y2+z)→c
Mặt khác
→AQ=→b+→a+t→B1D
=→a+→b+t(−→a−→b+→c)
=(1−t)→a+(1−t)→b+t→c
Ta có hệ phương trình sau:
{y=1−tx2+z=1−ty2+z=tx+y+z=1⇔{x2−y+z=0x+y+z=1x2+y2+2z=1⇒1−z=2−4z⇔z=13⇒x=29,y=49,t=59.
Vậy giao điểm Q của đường thẳng B1D với mp(CMN) được xác định bởi
→B1Q=59→B1D
b) Từ kết quả của câu a), ta có :
→AP=→a+→b+52→c→AQ=49→a+49→b+59→c.

