Đề bài
Cho hai đường thẳng a, b cắt nhau và không vuông góc với nhau, điểm O không nằm trên chúng. Hãy xác định điểm A nằm trên a và điểm B nằm trên b sao cho tam giác OAB vuông cân tại đỉnh O.
Lời giải chi tiết
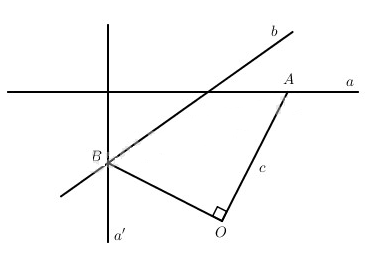
Giả sử đã xác định được hai điểm A, B theo yêu cầu của Câu toán.
Vì \(\widehat {AOB} = {90^0}\) nên góc lượng giác \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = \pm {\pi \over 2}\).
Xét trường hợp \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = {\pi \over 2}\).
Gọi Q là phép quay tâm O với góc quay \({\pi \over 2}\) và a’ là ảnh của đường thẳng a qua phép Q. Vì Q biến điểm A thành điểm B nên B cũng nằm trên đường thẳng a’, nói cách khác B là giao điểm của a’ và b.
Vậy ta có cách xác định điểm B như sau: Xác định đường thẳng a’ là ảnh của đường thanwgr a qua phéo quay Q rồi lấy giao điểm B của a’ và n. (Chú ý rằng a’ vuông góc với a còn b không vuông góc với a bên a’ và b cắt nhau).
Để xác định điểm A ta vẽ đường thẳng c đi qua O và vuông góc OB thì c sẽ cắt a tại A. Vậy OAB là tam giác vuông cân cần tìm.
Đối với trường hợp \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = - {\pi \over 2}\) ta cũng làm tương tự và được tam giác vuông cân OA’B’ với A’ nằm trên a và B’ nằm trên b.
Bài toán có hai nghiệm hình.

