Đề bài
Cho tứ diện ABCD. Gọi M là trung điểm của AB và N là một điểm thuộc cạnh CD không trùng với C và D. Mặt phẳng (P) qua MN và song song với BC.
a) Hãy xác định thiết diện của tứ diện khi cắt bởi mp(P).
b) Xác định vị trí của điểm N trên CD sao cho thiết diện là một hình bình hành.
Lời giải chi tiết
a) Mặt phẳng (ABC) chứa BC và BC //(P) nên (ABC) cắt (P) theo giao tuyến ME//BC(E∈AC). Tương tự, mp(DBC) cắt (P) theo giao tuyến NF//BC(F∈BD). (Dễ thấy E là trung điểm của AC). Thiết diện là hình thang MENF.
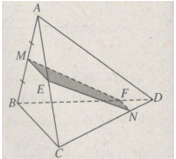
b) Từ câu a), ta có:
ME//NF và ME=12BC.
Vậy tứ giác MENF là hình bình hành khi và chỉ khi NF=ME=12BC hay N là trung điểm của CD.

