Đề bài
Cho hình hộp ABCD.A1B1C1D1. Gọi O1 là trọng tâm của hình bình hành A1B1C1D1; K là trung điểm của CD; E là trung điểm BO1.
a) Chứng minh rằng E nằm trên mp(ACB1).
b) Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng (P) qua điểm K và song song với mặt phẳng (EAC).
Lời giải chi tiết
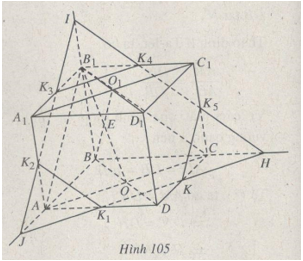
a) Gọi O là tâm của hình bình hành ABCD. Dễ thấy B1O1OB là hình bình hành, nên trung điểm E của đường chéo BO1 cũng là trung điểm của đường chéo OB1. Do đó E nằm trên OB1. Mà OB1 nằm trên mp(ACB1).Vậy E nằm trên mp(ACB1).
b) Theo câu a) thì mp(ACB1) cũng là mp(EAC). Do đó (P) là mặt phẳng qua K và song song với mp(ACB1). Từ K kẻ đường thẳng song song với AC cắt AD, AB, BC lần lượt tại K1, J, H. Từ J kẻ đường thẳng song song với AB1, cắt AA1, A1B1, BB1 lần lượt tại K2, K3, I. Nối I và H cắt B1C1, C1C tại K4 và K5.
Dễ thấy thiết diện là lục giác KK1K2K3K4K5 có các cạnh đối song song với nhau.

