Lựa chọn câu để xem lời giải nhanh hơn
Phép đối xứng qua điểm I(π2;0) biến đồ thị mỗi hàm số sau thành đồ thị của hàm số nào? Vẽ đồ thị của hàm số tìm được.
LG a
y=sinx
Phương pháp giải:
Điểm đối xứng của điểm M(x;y) qua điểm (π2;0) là điểm M′(x′;y′)
x′=π−x;y′=−y tức là x=π−x′,y=−y′.
Lời giải chi tiết:
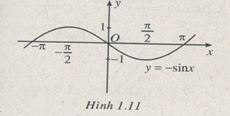
y=−sinx
LG b
y=cos2x
Phương pháp giải:
Điểm đối xứng của điểm M(x;y) qua điểm (π2;0) là điểm M′(x′;y′)
x′=π−x;y′=−y tức là x=π−x′,y=−y′.
Lời giải chi tiết:
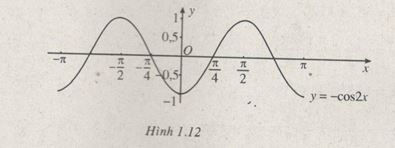
y=−cos2x (h.1.12)
LG c
y=sinx2
Phương pháp giải:
Điểm đối xứng của điểm M(x;y) qua điểm (π2;0) là điểm M′(x′;y′)
x′=π−x;y′=−y tức là x=π−x′,y=−y′.
Lời giải chi tiết:
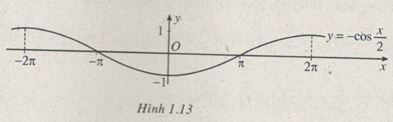
y=−cosx2 (h.1.13)