Trong mặt phẳng tọa độ, cho các đường thẳng \(({d_1})\) và \(({d_2})\) tương ứng với đồ thị của các hàm số \(y = 2x - 1\) và \(y = x.\)
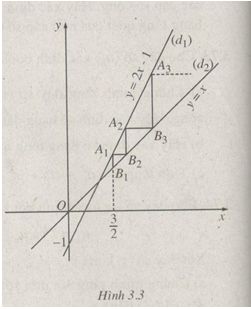
Xây dựng dãy các điểm \(({A_n})\) nằm trên \(({d_1})\) và dãy các điểm \(({B_n})\) nằm trên \(({d_2})\) theo cách sau (h.3.3):
\( \bullet \) \({A_1}\) và \({B_1}\) tương ứng là giao điểm của đường thẳng \(x = {3 \over 2}\) với \(({d_1})\) và \(({d_2})\);
\( \bullet \)Với mỗi số nguyên \(n \ge 2,{B_n}\) là giao điểm \(({d_2})\) với đường thẳng đi qua \({A_{n - 1}}\) và song song với trục hoành, \({A_n}\) là giao điểm của điểm \(({d_1})\) với đường đi qua \({B_n}\) và song song với trục tung.
Với mỗi số nguyên dương n, kí hiệu \({u_n}\) là hoành độ của \({A_n}\) và \({h_n}\) là độ dài của đoạn thẳng \({A_n}{B_n}\).
LG a
Chứng minh rằng dãy số \(({h_n})\) là một cấp số nhân. Hãy xác định số hạng đầu và công bội của cấp số nhân đó.
Lời giải chi tiết:
Với mỗi \(n \ge 1,\) kí hiệu \({a_n}\) và \({b_n}\) tương ứng với tung độ của điểm \({A_n}\) và điểm \({B_n}.\) Khi đó :
- Do \({A_n}\) nằm trên \(\left( {{d_1}} \right)\) nên \({a_n} = 2{u_n} - 1.\)
- Do \({B_n}\) là giao điểm của \(\left( {{d_2}} \right)\) và đường thẳng đi qua \({A_n}\), song song với trục tung \({b_n} = {u_n}\). Suy ra với mọi \(n \ge 1.\)
\({h_n} = {a_n} - {b_n} = \left( {2{u_n} - 1} \right) - {u_n} \)\(= {u_n} - 1\,\,(1)\)
Hơn nữa, với mỗi \(n \ge 1,\) do \({B_{n + 1}}\) nằm trên đường thẳng đi qua \({A_n}\) và song song với trục hoành nên \({b_{n + 1}} = {a_n} = 2{u_n} - 1\). Suy ra \({u_{n + 1}} = 2{u_n} - 1\) với mỗi \(n \ge 1.\)
Từ đó ta được \({u_{n + 1}} - 1 = 2({u_n} - 1)\) với mọi \(n \ge 1,\) hay \({h_{n + 1}} = 2{h_n}\) với mọi \(n \ge 1\,\,\left( {theo\left( 1 \right)} \right).\) Vì thế, \(\left( {{h_n}} \right)\) là một cấp số nhân với số hạng đầu
\({h_1} = {u_1} - 1 = {3 \over 2} - 1 = {1 \over 2}\) và công bội \(q = 2\)
LG b
Dựa vào kết quả phần a), hãy xác định số hạng tổng quát của dãy số \(({u_n})\).
Lời giải chi tiết:
Ta có \({h_n} = {h_1}.{q^{n - 1}} = {1 \over 2} \times {2^{n - 1}} = {2^{n - 2}}\) với mọi \(n \ge 1.\) Suy ra
\({u_n} = {h_n} + 1 = {2^{n - 2}} + 1\) với mọi \(n \ge 1.\)

