Đề bài
Cho tam giác đều ABC với (AB, AC) = (BC, BA) = (CA, CB) = \({60^o}.\) Gọi \({Q_A},\,{Q_B}\) là các phép quay góc \({60^o}\) lần lượt có tâm là A và B. Gọi F là hợp thành của \({Q_B}\) và \({Q_A}.\)
a) Phép F biến các điểm A, B, C thành các điểm nào?
b) Phép F là phép gì?
c) Phép hợp thành của \({Q_A}\) và \({Q_B}\) là phép gì?
Lời giải chi tiết
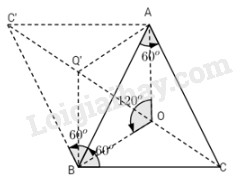
a) Ta gọi C’ là điểm đối xứng với điểm C qua AB.
Phép quay \({Q_B}\) biến A thành C’, B thành B và biến C thành A.
Phép quay \({Q_A}\) biến C’ thành B, biến B thành C và biến A thành A.
Vậy hợp thành F là phép dời hình biến ba điểm A, B, C lần lượt thành ba điểm B, C, A.
b) Từ câu a), suy ra : Nếu gọi O là tâm tam giác đều ABC thì F là phép quay tâm O góc quay \({120^o}.\)

