Đề bài
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên SAB là tam giác cân tại S và mp(SAB) vuông góc với mp(ABCD), cạnh SC tạo với mặt phẳng đáy góc α. Tính:
a) Chiều cao của hình chóp S.ABCD;
b) Khoảng cách từ chân đường cao hình chóp đến mặt phẳng (SCD);
c) Diện tích thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng trung trực của cạnh BC.
Lời giải chi tiết
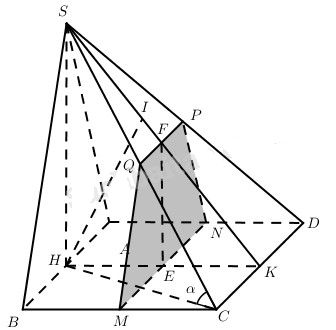
a) Gọi H là trung điểm của AB thì \(SH \bot AB\), từ đó \(SH \bot \left( {ABC{\rm{D}}} \right)\). Vậy khoảng cách từ S đến mp(ABCD) là SH, đó là chiều cao của hình chóp.
Ta có \(SH = HC\tan \alpha \),
mặt khác \(H{C^2} = B{H^2} + B{C^2} = {{5{{\rm{a}}^2}} \over 4}\).
hay \(HC = {{a\sqrt 5 } \over 2}\).
Vậy \(SH = {{a\sqrt 5 } \over 2}\tan \alpha \).
b) Gọi K là trung điểm của CD thì \(C{\rm{D}} \bot \left( {SHK} \right)\), từ đó \(\left( {SC{\rm{D}}} \right) \bot \left( {SHK} \right)\). Vậy nếu kẻ đường cao HI của tam giác SHK thì HI là khoảng cách từ H đến mp(SCD). Ta có:
\(\eqalign{ & HI = {{H{\rm{S}}.HK} \over {SK}} = {{{{a\sqrt 5 } \over 2}\tan \alpha .a} \over {\sqrt {{{5{{\rm{a}}^2}} \over 4}{{\tan }^2}\alpha + {a^2}} }} \cr & = {{a\sqrt 5 \tan \alpha } \over {\sqrt {5{{\tan }^2}\alpha + 4} }} \cr} \)
c) Vì SH và CD cùng vuông góc với BC nên SH, CD song song với mặt phẳng trung trực (R) của BC. Khi đó:
\(\left( R \right) \cap \left( {ABC{\rm{D}}} \right) = MN\) với MN // CD và M, N lần lượt là trung điểm của BC, AD.
\(\left( R \right) \cap \left( {SHK} \right) = EF\), EF // SH, E là trung điểm của MN.
\(\left( R \right) \cap \left( {SC{\rm{D}}} \right) = PQ\), PQ đi qua điểm F và PQ // CD. Thiết diện MNPQ là hình thang cân.
Ta có
\(\eqalign{ & {S_{MNPQ}} = {1 \over 2}\left( {MN + PQ} \right).EF \cr & = {1 \over 2}\left( {a + {a \over 2}} \right).{{a\sqrt 5 } \over 4}\tan \alpha \cr & = {{3{a^2}\sqrt 5 } \over {16}}\tan \alpha \cr} \).

