Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC, N là trung điểm của OB (O là giao điểm của BD và AC).
a) Tìm giao điểm I của SD và mặt phẳng (AMN).
b) Tính tỉ số SIID.
Lời giải chi tiết
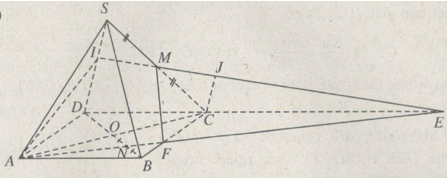
a) Kéo dài AN cắt DC tại E. Nối E và M cắt SD tại I, thế thì I chính là giao điểm của SD và mp(AMN).
b) Gọi F là giao điểm của AN và BC.
BF//AD⇒BFAD=NBND=13
Từ
BFAD=13⇒FCAD=23⇒ECED=FCAD=23
Kẻ CJ//SD(J∈EI). Ta có:
MCMS=CJJS,IDCJ=EDEC⇒ISID=MSMC.ECED=1.23=23
Vậy ISID=23.

