Cho hàm số
f(x)=x3−2x2+mx−3
Tìm m để
LG a
f′(x) bằng bình phương của một nhị thức bậc nhất;
Lời giải chi tiết:
Với mọi x∈R, ta có
f′(x)=3x2−4x+m
Để f′(x) bằng bình phương của một nhị thức bậc nhất ta phải tìm m sao cho f′(x) phải là tam thức bậc hai ax2+bx+c với hệ số a>0 và có nghiệm kép, tức là
{a=3>0Δ′=4−3m=0⇔m=43
LG b
f′(x)≥0 với mọi x;
Lời giải chi tiết:
Để f′(x)≥0 với mọi x thì ta phải tìm m sao cho
{a=3>0Δ′=4−3m≤0⇔m≥43
LG c
f′(x)<0 với mọi x∈(0;2)
Lời giải chi tiết:
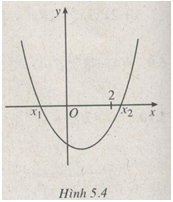
(h.5.4) Để f′(x)<0 với mọi x∈(0;2) thì ta phải tìm m sao cho số 0 và số 2 thuộc đoạn [x1;x2] (x1 và x2 là hai nghiệm của của f′(x)) tức là
{af′(0)≤0af′(2)≤0⇔{3.m≤03(4+m)≤0⇔m≤−4.
LG d
f′(x)>0 với mọi x>0
Lời giải chi tiết:
Để f′(x)>0 với mọi x>0 thì ta phải xét hai trường hợp sau đây
∙ Trường hợp thứ nhất (h.5.5a)
Ta phải tìm m sao cho tam thức bậc hai f′(x) vô nghiệm và có a>0, tức là
{a=3>0Δ′=4−3m<0⇔m>43.
∙ Trường hợp thứ hai (h.5.5b)
Ta phải tìm m sao cho tam thức bậc hai f′(x) có a>0 đồng thời có hai nghiệm x1 và x2 thỏa mãn các điều kiện x1≤x2≤0, tức là
{a=3>0Δ′=4−3m≥0af′(0)=3m≥0S2−0=23≤0( loại )
Hệ vô nghiệm.
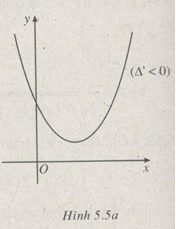
Chú ý. Về nguyên tắc phải xét hai trường hợp, dù trong bài này trường hợp thứ hai vô nghiệm.
