Đề bài
Cho hình vuông ABCD. Gọi S là điểm trong không gian sao cho SAB là tam giác đều và mp(SAB) vuông góc với mp(ABCD).
a) Chứng minh rằng mp(SAB)⊥mp(SAD) và mp(SAB)⊥mp(SBC).
b) Tính góc giữa hai mặt phẳng (SAD) và (SBC).
c) Gọi H và I lần lượt là trung điểm của AB và BC. Chứng minh rằng
mp(SHC)⊥mp(SDI).
Lời giải chi tiết
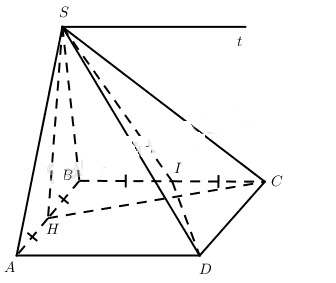
a) Gọi H là trung điểm của AB thì SH⊥AB.
Do (SAB)⊥(ABCD) nên SH⊥(ABCD)⇒SH⊥AD, mặt khác AD⊥AB.
Vậy AD⊥(SAB).
Từ đó (SAD)⊥(SAB).
Tương tự như trên, ta có:
(SBC)⊥(SAB)
b) Giả sử (SAD)∩(SBC)=St, dễ thấy St // AD, từ đó mp(ASB)⊥St. Do ^ASB=600 nên góc giữa hai mặt phẳng (SAD) và (SBC) bằng 60°.
c) Vì ABCD là hình vuông; H, I lần lượt là trung điểm của AB và BC nên HC⊥DI, mặt khác DI⊥SH. Vậy DI⊥(SHC), từ đó (SDI)⊥(SHC).

