Đề bài
Cho tứ diện ABCD, đáy là tam giác cân và \(DA \bot mp\left( {ABC} \right),AB = AC = a,BC = {6 \over 5}a\). Gọi M là trung điểm của BC. Vẽ AH vuông góc với MD (H thuộc đường thẳng MD).
a) Chứng minh rằng \(AH \bot mp\left( {BC{\rm{D}}} \right)\).
b) Cho \(A{\rm{D}} = {4 \over 5}a\). Tính góc giữa hai đường thẳng AC và DM.
c) Gọi G1, G2 lần lượt là các trọng tâm của tam giác ABC và tam giác DBC. Chứng minh rằng \({G_1}{G_2} \bot mp\left( {ABC} \right)\).
Lời giải chi tiết
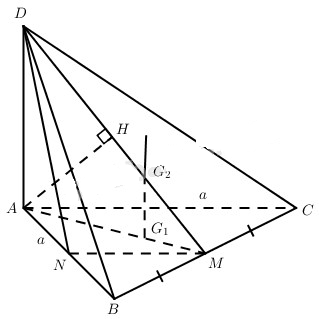
a) Vì M là trung điểm của BC nên \(AM \bot BC\), mặt khác \(DA \bot \left( {ABC} \right)\) nên BC vuông góc với mp(DAM), từ đó \(BC \bot AH\).
Mà \(DM \bot AH\).
Vậy \(AH \bot mp\left( {DBC} \right)\).
b) Kẻ MN song song với AC (N ∈ AB) thì góc giữa DM và AC bằng góc giữa DM và MN, đó là \(\widehat {DMN}\) hoặc \({180^0} - \widehat {DMN}\).
Ta có:
\(\eqalign{ & MN = {1 \over 2}AC = {a \over 2},AN = {a \over 2}. \cr & D{N^2} = D{A^2} + A{N^2} = {{16} \over {25}}{a^2} + {{{a^2}} \over 4} = {{89} \over {100}}{a^2} \cr & A{M^2} = A{B^2} - B{M^2} = {a^2} - {{9{{\rm{a}}^2}} \over {25}} = {{16{{\rm{a}}^2}} \over {25}} \cr & \Rightarrow AM = {{4{\rm{a}}} \over 5}. \cr} \)
Mặt khác \(A{\rm{D}} = {{4{\rm{a}}} \over 5}\) do đó \(DM = {{4{\rm{a}}\sqrt 2 } \over 5}\).
\(\eqalign{ & D{N^2} = D{M^2} + M{N^2} - 2{\rm{D}}M.MN\cos \widehat {DMN} \cr & {{89} \over {100}}{a^2} = {{2.16{a^2}} \over {25}} + {{{a^2}} \over 4} - 2.{{4a\sqrt 2 } \over 5}.{a \over 2}\cos \widehat {DMN} \cr & = {{153{a^2}} \over {100}} - {{4{a^2}\sqrt 2 } \over 5}\cos \widehat {DMN} \cr & \Rightarrow {{4{a^2}\sqrt 2 } \over 5}\cos \widehat {DMN} = {{64{a^2}} \over {100}} \cr & \Rightarrow \cos \widehat {DMN} = {{2\sqrt 2 } \over 5}. \cr} \).
Vậy góc giữa AC và DM là α mà \(\cos \alpha = {{2\sqrt 2 } \over 5}\) .
c) Dễ thấy G1G2 // DA mà DA ⊥ (ABC) nên \({G_1}{G_2} \bot \left( {ABC} \right)\).

