Đề bài
Cho tứ diện ABCD có \(BC = B{\rm{D}} = AC = A{\rm{D}};AB = a,C{\rm{D}} = a\sqrt 3 \). Gọi I và J lần lượt là trung điểm của AB và CD, IJ = a.
a) Chứng minh rằng IJ là đường vuông góc chung của AB và CD.
b) Tính khoảng cách từ điểm cách đều bốn đỉnh A, B, C, D đến mỗi đỉnh đó.
Lời giải chi tiết
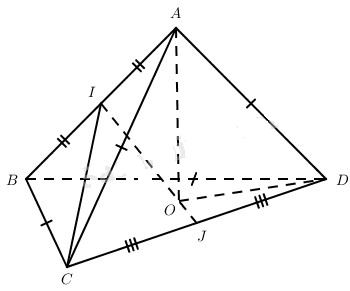
a)
\(\eqalign{
& \Delta BCD = \Delta ACD(c.c.c) \cr
& \Rightarrow BJ =AJ \cr} \)
Do đó \(\Delta ABJ\) cân tại J, suy ra \(IJ \bot AB\)
Chứng minh tương tự: \(IJ \bot CD\)
Vậy IJ là đường vuông góc chung của AB và CD.
b) Gọi O là điểm cách đều các đỉnh A, B, C, D thì O thuộc đường thẳng IJ. Khi đó OA = OD. Điều này xảy ra khi và chỉ khi \(I{A^2} + O{I^2} = O{J^2} + J{D^2}\), đặt \(I{\rm{O}} = x\) ta có đẳng thức
\(\eqalign{ & {{{a^2}} \over 4} + {x^2} = {\left( {a - x} \right)^2} + {\left( {{{a\sqrt 3 } \over 2}} \right)^2} \cr & \Leftrightarrow x = {3 \over 4}a \cr} \)
Như vậy khoảng cách từ điểm O đến mỗi đỉnh của tứ diện ABCD bằng
\(\sqrt {{{{a^2}} \over 4} + {{9{{\rm{a}}^2}} \over {16}}} = {{a\sqrt {13} } \over 4}\).

