Đề bài
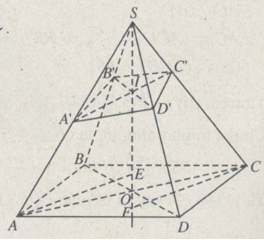
Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) lần lượt cắt các cạnh SA, SB, SC tại A’, B’, C’. Gọi O là giao điểm của AC và BD; I là giao điểm của A’C’ và SO.
a) Tìm giao điểm D’ của mp(P) với cạnh SD.
b) Chứng minh rằng SASA′+SCSC′=2SOSI
c) Chứng minh rằng SASA′+SCSC′=SBSB′+SDSD′.
Lời giải chi tiết
a) Trong mp(SAC) nối A’ với C’ cắt SO tại I. Trong mp(SBD) nối B’ với I cắt SD tại D’. Khi đó D’ chính là giao điểm của mp(P) với SD.
b) (h.126)
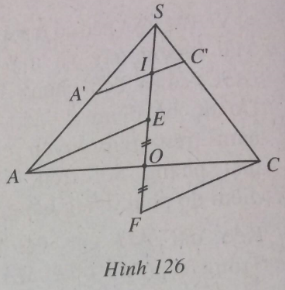
Trong mp(SAC), kẻ AE // A'C' cắt SO tại E; kẻ CF // A'C' cắt SO tại F. Ta có:
SASA′=SESI=SO−OESI(1)
SCSC′=SFSI=SO+OFSI(2)
Do O là trung điểm của AC và AE // CF, nên OE = OF.
Vậy từ (1) và (2), suy ra SASA′+SCSC′=2SOSI (3)
c) Chứng minh tương tự câu b), ta có:
SBSB′+SDSD′=2SOSI (4)
Từ (3) và (4), suy ra:
SASA′+SCSC′=SBSB′+SDSD′.

