Đề bài
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Lấy điểm M thuộc đoạn thẳng AD’, điểm N thuộc đoạn thẳng BD sao cho
AM=DN=x(0<x<a√2)
a) Tìm x để đoạn thẳng MN có độ dài ngắn nhất.
b) Khi MN ngắn nhất, hãy chứng tỏ MN là đường vuông góc chung của AD’ và DB, đồng thời MN // A’C.
Lời giải chi tiết
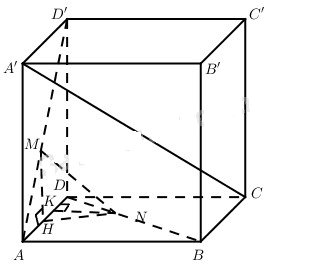
a) Kẻ MH⊥AD thì MH⊥(ABCD) và MH=x√22=AH.
Kẻ NK⊥AD thì NK=x√22=DK.
Vậy KH=|a−x√2|.
Ta có:
MN2=MH2+HK2+KN2=3x2−2a√2x+ah2
Từ đó MN nhỏ nhất khi và chỉ khi x=a√23.
b) Khi x=a√23 thì
MN2=3a29=a23;AM2=2a29;AN2=AD2+DN2−2AD.DNcos450=5a29
Từ đó AN2=AM2+MN2 hay MN⊥AD′.
Chứng minh tương tự như trên, ta cũng có MN⊥BD.
Vậy MN là đường vuông góc chung của AD’ và BD.
Khi DN=a√23 thì NB = 2ND.
Gọi I là trung điểm của AD thì ta có I, N, C thẳng hàng
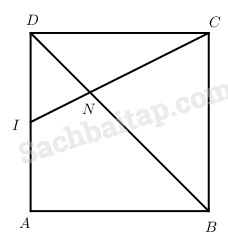
Tương tự ta cũng có các điểm I, M, A’ thẳng hàng.
Xét tam giác A’IC ta có:
INNC=IMMA′=12
Vậy MN // A’C.

