Cho hai phép vị tự V1 có tâm O1 tỉ số k1 và V2 có tâm O2 tỉ số k2. Gọi F là hợp thành của V1 và V2. Chứng minh rằng:
LG a
F là một phép tịnh tiến nếu k1k2 = 1. Hãy xác định vec tơ tịnh tiến.
Lời giải chi tiết:
Lấy một điểm M bất kỳ, nếu V1 biến M thành M1 và V2 biến M1 thành M2 thì \(\overrightarrow {{O_1}{M_1}} = {k_1}\overrightarrow {{O_1}M} \) và \(\overrightarrow {{O_2}{M_2}} = {k_2}\overrightarrow {{O_2}{M_1}} \).
Khi đó, phép hợp thành F biến M thành M2. Gọi I là ảnh của O1 qua phép vị tự V2, tức là \(\overrightarrow {{O_2}I} = {k_2}\overrightarrow {{O_2}{O_1}} \).
Khi đó \(\overrightarrow {I{M_2}} = {k_2}\overrightarrow {{O_1}{M_1}} = {k_1}{k_2}\overrightarrow {{O_1}M} \).
(h.33)
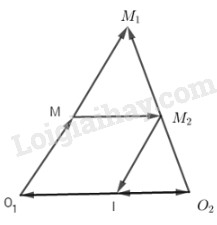
Nếu k1k2 = 1 thì \(\overrightarrow {I{M_2}} = \overrightarrow {{O_1}M} \) nên \(\overrightarrow {M{M_2}} = \overrightarrow {{O_1}I} = \overrightarrow {{O_1}{O_2}} + \overrightarrow {{O_2}I} = \left( {1 - {k_2}} \right)\overrightarrow {{O_1}{O_2}} \).
Vậy trong trường hợp này F là phép tịnh tiến vectơ \(\overrightarrow u = \left( {1 - {k_2}} \right)\overrightarrow {{O_1}{O_2}} \).
LG b
F là một phép vị tự nếu k1k2 1. Hãy xác định tâm và tỉ số của phép vị tự đó.
Lời giải chi tiết:
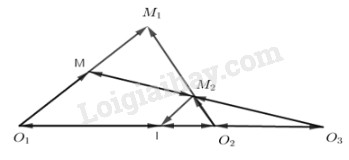
Nếu k1k2 \(\ne\) 1 ta chọn điểm O3 sao cho \(\overrightarrow {{O_3}I} = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} \)
Khi đó \(\overrightarrow {{O_3}{M_2}} = \overrightarrow {{O_3}I} + \overrightarrow {I{M_2}} \)
\( = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} + {k_1}{k_2}\overrightarrow {{O_1}M} \)
\( = {k_1}{k_2}\overrightarrow {{O_3}M} \)
Vậy F là phép vị tự tâm O3 tỉ số \({k_1}{k_2}\).
Chú ý rằng tâm O3 của phép vị tự đó được xác định bởi đẳng thức:
\(\overrightarrow {{O_3}I} = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} \)
Hay \(\overrightarrow {{O_3}{O_1}} + \overrightarrow {{O_1}{O_2}} + \overrightarrow {{O_2}I} = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} \).
Suy ra: \(\overrightarrow {{O_1}{O_2}} + {k_2}\overrightarrow {{O_2}{O_1}} = \left( {1 - {k_1}{k_2}} \right)\overrightarrow {{O_1}{O_3}} \).
Do đó: \(\overrightarrow {{O_1}{O_3}} = {{1 - {k_2}} \over {1 - {k_1}{k_2}}}\overrightarrow {{O_1}{O_2}} \).
Cũng chú ý rằng tâm của ba phép vị tự V1, V2 và F là ba điểm thẳng hàng O1, O2 và O3.

