Cho Đ là phép đối xứng trục có trục đối xứng là đường thẳng d và T là phép tịnh tiến theo vectơ \(\overrightarrow v \) song song với d. Hợp thành Đ và T gọi là phép đối xứng trượt. Phép đối xứng trục là một trường hợp đặc biệt của phép đối xứng trượt khi vectơ trượt là vectơ không.
LG a
Chứng minh rằng hợp thành của T và Đ cũng bằng hợp thành của Đ và T.
Lời giải chi tiết:
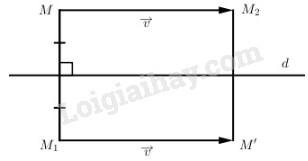
Giả sử M là một điêmt nào đó, Đ biến M thành M1 và T biến M1 thành M’.
Như vậy, nếu gọi F là hợp thành của T và Đ thì F biến M thành M’.
Nếu ta lấy điểm M2 sao cho MM1M’M2 là hình chữ nhật thì rõ ràng T biến M thành M2 và Đ biến M2 thành M’.
Vậy F cũng là hợp thành của T và Đ.
LG b
Chứng minh rằng nếu M’ là ảnh của M qua phép đối xứng trượt thì trung điểm đoạn thẳng MM’ luôn nằm trên trục của phép đối xứng trượt đó.
Lời giải chi tiết:
Hiển nhiên
LG c
Hợp thành của hai phép đối xứng trượt có trục song song là phép gì?
Lời giải chi tiết:
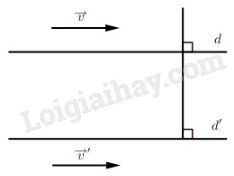
Giả sử phép đối xứng trượt F có trục d và vectơ trượt \(\overrightarrow v \) , phép đối xứng trượt F’ có trục đối xứng d’ và véc tơ trượt \(\overrightarrow v '\) .
Kí hiệu Đ, Đ’ lần lượt là phép đối xứng có trục d và d’, T và T’ lần lượt là các phép tịnh tiến theo vectơ \(\overrightarrow v \) và \(\overrightarrow {v'} \) .
Như vậy F là hợp thành của T và Đ, F’ là hợp thành của Đ’ và T’.
Suy ra hợp thành của F và F’ là hợp thành của bốn phép: T, Đ, Đ’ và T’.
Vì d // d’ nên hợp thành của Đ và Đ’ là một phép tịnh tiến.
Vậy hợp thành F và F’ là hợp thành của ba phép tịnh tiến và do đó là môt phép tịnh tiến.
LG d
Chứng minh rằng hợp thành của một phép đối xứng trục và một phép tịnh tiến là một phép đối xứng trượt.
Lời giải chi tiết:
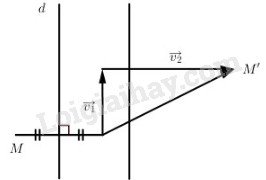
Gọi Đ là phép đối xứng trục, với trục là đường thẳng d, T là phép tịnh tiến theo vectơ \(\overrightarrow v \) , còn F là hợp thành của Đ và T.
Ta có thể tìm được hai vectơ \(\overrightarrow {{v_1}} \) và \(\overrightarrow {{v_2}} \) sao cho \(\overrightarrow {{v_1}} \) song song với d, \(\overrightarrow {{v_2}} \) vuông góc với d và \(\overrightarrow v = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} \) .
Nếu ta gọi T1 và T2 lần lượt là các phép tịnh tiến theo các vectơ \(\overrightarrow {{v_1}} \) và \(\overrightarrow {{v_2}} \) thì T là hợp thành của T2 và T1.
Nhưng vì \(\overrightarrow {{v_2}} \) vuông góc với d nên T2 có thể xem là hợp thành của hai phép đối xứng trục D1 và D2 có trục song song với d. Tóm lại, F là hợp thành của bốn phép Đ, Đ1, Đ2 và T1.
Như đã biết, hợp thành của 3 phép đối xứng trục Đ, Đ1, Đ2 (có trục song song) là phép đối xứng của trục Đ3 có trục song song với d. Vậy F là hợp thành của Đ3 và T1 với vectơ tịnh tiến của T1 song song với trục đối xứng Đ3, nên F là phép đối xứng trượt.
LG e
Chứng minh rằng hợp thành của một phép quay và một phép đối xứng trục là một phép đối xứng trượt.
Lời giải chi tiết:
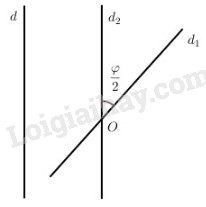
Giả sử Q là phép quay tâm O và Đ là phép đối xứng qua đường thẳng d, F là hợp thành của Q và Đ.
Ta có thể xem phép quay Q là hợp thành của hai phép đối xứng Đ1 và Đ2 có các trục đối xứng đi qua O, trong đó trục của Đ2 song song với d.
Như vậy F là hợp thành của ba phép đối xứng: Đ1, Đ2 và Đ.
Nhưng hợp thành của Đ2 và Đ (có trục đối xứng song song) là phép tịnh tiến do đó F là hợp thành của một phép đối xứng và một phép tịnh tiến nên theo câu d), F là phép đối xứng trượt.
LG g
Chứng minh rằng hợp thành của ba phép đối xứng trục là một phép đối xứng trượt.
Lời giải chi tiết:
Suy từ câu d và câu e).
