Đề bài
Cho tứ diện ABCD. Gọi E là điểm đối xứng của A qua điểm C. Xác định thiết diện của hình tứ diện khi cắt bởi mặt phẳng đi qua B, E và một điểm F trong các trường hợp sau đây:
a) F nằm trên đoạn CD và không trùng với C và D.
b) F nằm trong tam giác ACD.
c) F nằm trong đoạn thẳng DD’ (D’ là trọng tâm của tam giác ABC).
Lời giải chi tiết
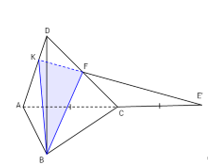
a) Trong mp(ACD), kéo dài EF cắt AD tại K. Khi đó thiết diện cần tìm là tam giác BFK.
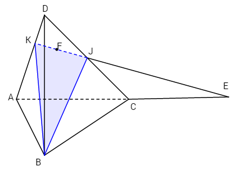
b) Trong mp(ACD) kéo dài EF cắt AD và DC lần lượt tại K và J. Khi đó thiết diện cần tìm tam giác BKJ.
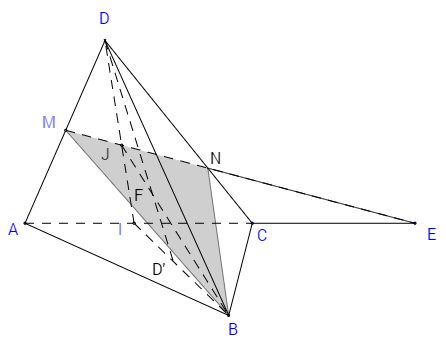
c) Gọi I là giao điểm của BD’ và AC (I là trung điểm của AC). Xét mp(BDI) ta có đường thẳng BF cắt DI tại một điểm J. Khi đó J là điểm chung của hai mặt phẳng (BEF) và (DAC).
Vậy (BEF) cắt (DAC) theo đường thẳng EJ. Đường thẳng này cắt AD và DC tại M và N.
Vậy thiết diện cần tìm là tam giác BMN.