Đề bài
Về phía ngoài của hình bình hành ABCD dựng các hình vuông có cạnh lần lượt là AB, BC, CD, DA. Chứng minh rằng bốn tâm của bốn hình vuông đó là đỉnh của một hình vuông.
Lời giải chi tiết
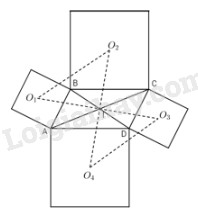
Gọi \({O_1},\,{O_2},\,{O_3},\,{O_4}\) là tâm các hình vuông có cạnh lần lượt là AB, BC, CD, DA.
Gọi I là tâm hình bình hành ABCD thì I là tâm đối xứng của hình gồm hình bình hành và bốn hình vuông đã cho. Bởi vậy I là trung điểm của \({O_1}{O_3}\) và \({O_2}{O_4}.\)
Nói cách khác \({O_1}{O_2}{O_3}{O_4}\) là hình bình hành.
Xét tam giác ABC, theo kết quả bài tập 43 ta có \(I{O_1}{O_2}\) là tâm giác vuông cân.
Vậy \({O_1}{O_2}{O_3}{O_4}\) là hình vuông.

