Đề bài
Cho tam giác ABC. Gọi A’, B’, C’ lần lượt là tâm của đường tròn bàng tiếp trong góc A, góc B và góc C. Chứng minh rằng các đường thẳng đi qua A’ vuông góc với BC, qua B’ vuông góc với AC, qua C’ vuông góc với AB đồng quy.
Lời giải chi tiết
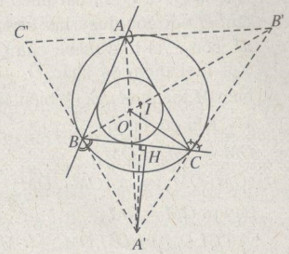
Trước hết, dễ thấy rằng các điểm A, B, C lần lượt nằm trên các cạnh B’C’, C’A’, A’B’ của tam giác A’B’C’ và các đường thẳng AA’, BB’, CC’ đi qua tâm O của đường tròn nội tiếp tam giác ABC.
Kẻ \(A'H \bot BC\,\left( {H \in BC} \right)\) ta có:
\(\widehat {CA'H} = \widehat {OCB}\)
(góc có cạnh tương ứng vuông góc) và
\(\widehat {OCB} = \widehat {BA'O}\)
(do tứ giác OBA’C nội tiếp đường tròn).
Từ đó, suy ra:
\(\widehat {CA'H} = \widehat {BA'O}\)
Do đó, nếu gọi I là tâm đường tròn nội tiếp tam giác A’B’C’ thì AI’ là phân giác góc B’A’C’ nên A’H đối xứng với A’O qua đường thẳng A’I. Bởi vậy A’H đi qua điểm đối xứng với O qua phân giác A’I.
Tương tự ta cũng có đường thẳng đi qua B’, vuông góc với AC cũng đi qua điểm đối xứng với O qua B’I và đường thẳng đi qua C’, vuông góc với AB cũng đi qua điểm đối xứng với O qua C’I.
Từ đó áp dụng bài tập 28 ta suy ra điều phải chứng minh.
