Đề bài
Cho tứ diện ACBD. Gọi I và J lần lượt là trung điểm của BC và BD; E là một điểm thuộc cạnh AD khác với A và D.
a) Xác định thiết diện của tứ diện khi cắt bởi mp(IJE).
b) Tìm vị trí của điểm E trên AD sao cho thiết diện là hình bình hành.
c) Tìm điều kiện của tứ giác ABCD và vị trí của điểm E trên cạnh AD để thiết diện là hình thoi.
Lời giải chi tiết
a) Ta có IJ là đường trung bình của tam giác BCD nên IJ//CD.
Mặt khác \(IJ \subset \left( {IJE} \right);\,\,CD \subset \left( {ACD} \right)\) suy ra mp(IJE) cắt mp(ACD) theo giao tuyến Ex//CD. Gọi F là giao điểm của Ex và AC. Thiết diện là hình thang EFIJ.
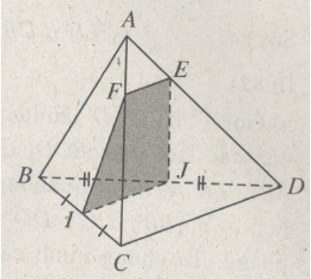
b) Để thiết diện EFIJ là hình bình hành điều kiện cần và đủ là IF // JE.
Điều này tương đương với JE //AB tức là khi và chỉ khi E là trung điểm của AD.
c) Thiết diện EFIJ là hình thoi \( \Leftrightarrow \) EFIJ là hình bình hành và IF = IJ \( \Leftrightarrow \) E là trung điểm của AD và AB = CD (vì \(IJ = {1 \over 2}CD\) và khi E là trung điểm của AD thì \(IF = {1 \over 2}AB\)).

