Đề bài
Hãy dùng định lí Ta-lét để giải bài tập 31 (chương II).
Lời giải chi tiết
(h.102)
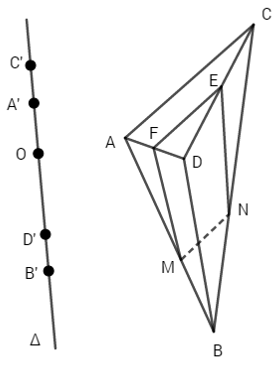
a) Ta vẽ một đường thẳng \(\Delta\) bất kì cắt mặt phẳng (MNEF) tại một điểm O.
Bốn mặt phẳng lần lượt qua A, B, C, D và đồng thời song song với mặt phẳng (MNEF) cắt đường thẳng \(\Delta\) theo thứ tự A’, B’, C’ và D’. Theo định lí Ta-lét ta có:
\({{MA} \over {MB}} = {{OA'} \over {OB'}}\), \({{NB} \over {NC}} = {{OB'} \over {OC'}}\)
\({{EC} \over {ED}} = {{OC'} \over {OD'}}\), \({{FD} \over {FA}} = {{OD'} \over {OA'}}\)
Vậy:
\({{MA} \over {MB}}.{{NB} \over {NC}}.{{EC} \over {ED}}.{{FD} \over {FA}} = {{OA'} \over {OB'}}.{{OB'} \over {OC'}}.{{OC'} \over {OD'}}.{{OD'} \over {OA'}} = 1\)

