Đề bài
Cho tứ diệm ABCD trong đó góc giữa hai đường thẳng AB và CD bằng α. Gọi M là điểm bất kì thuộc cạnh AC, đặt AM = x (0< x < AC). Xét mặt phẳng (P) đi qua điểm M và song song với AB, CD.
a) Xác định vị trí điểm M để diện tích thiết diện của hình tứ diện ABCD khi cắt bởi mp(P) đạt giá trị lớn nhấ.
b) Chứng minh rằng chu vi thiết diện nêu trên không phụ thuộc vào x khi và chỉ khi AB = CD.
Lời giải chi tiết
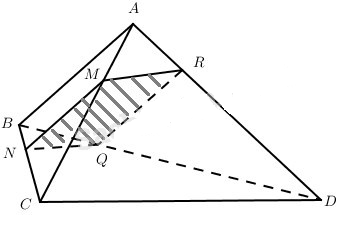
a) Dễ thấy thiết diện là hình bình hành MNPQ và \({S_{MNPQ}} = NM.NQ.\sin \widehat {MNQ}\) .
Do MN // AB, NQ // CD nên góc giữa MN và NQ bằng góc giữa AB và CD do đó \(\sin \widehat {MNQ} = \sin \alpha \) .
Ta có:
\(\eqalign{& {{MN} \over {AB}} = {{AC - x} \over {AC}} \Rightarrow MN = {{AB} \over {AC}}\left( {AC - x} \right) \cr
& NQ = M{\rm{R}},{{M{\rm{R}}} \over {C{\rm{D}}}} = {{AM} \over {AC}} = {x \over {AC}} \cr
& \Rightarrow M{\rm{R}} = {{C{\rm{D}}} \over {AC}}x \cr} \)
Vậy \({S_{MNQR}} = {{AB.CD} \over {A{C^2}}}\left( {AC - x} \right)x\sin \alpha \).
Từ đó diện tích thiết diện MNQR đạt giá trị lớn nhất khi và chỉ khi \(x = {{AC} \over 2}\).
Như vậy, khi M là trung điểm của AC thì diện tích thiết diện của tứ diện ABCD cắt bởi (P) đạt giá trị lớn nhất.
b) Gọi P là nửa chu vi của thiết diện, khi đó:
\(\eqalign{ & p = MN + M{\rm{R}} = {{AB} \over {AC}}\left( {AC - x} \right) + {{C{\rm{D}}} \over {AC}}x \cr & = {{C{\rm{D}} - AB} \over {AC}}x + AB \cr} \)
Từ đó, chu vi thiết diện không phụ thuộc vào x khi và chỉ khi:
\(CD – AB = 0\) hay \(AB = CD.\)

