Đề bài
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến ∆ và tạo với nhau góc α. Xét hai điểm M và N lần lượt thuộc (P) và (Q). Kẻ MI vuông góc với ∆, NJ vuông góc với ∆. Cho biết MI=a,NJ=b,IJ=c. Tính độ dài MN.
Lời giải chi tiết
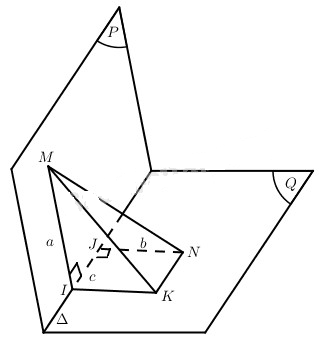
Trong mp(Q), kẻ qua I đường thẳng song song với JN và kẻ qua N đường thẳng song song với IJ, chúng cắt nhau tại K.
Dễ thấy MI⊥NK, tứ giác IJNK là hình chữ nhật.
Như vậy MI⊥NK,IK⊥KN, từ đó MK⊥KN, ngoài ra IK = b, NK = c.
Vì MI và IK cũng vuông góc với IJ.
Vậy ^MIK hoặc 1800−^MIK là góc giữa hai mặt phẳng (P) và (Q).
Ta có:
MN2=MK2+KN2=MK2+c2;MK2=a2+b2−2abcos^MIK
Vậy MN=√a2+b2−2abcos^MIK+c2
hoặc MN=√a2+b2+2abcos^MIK+c2.

