Đề bài
Cho hình hộp ABCD.A’B’C’D’. Điểm M thuộc cạnh AD, điểm N thuộc cạnh D’C’ sao cho AM : MD = D’N : NC’
a) Chứng minh rằng MN song song với (C’BD)
b) Xác định thiết diện của hình hộp khi cắt bởi mp(P) qua MN và song song với mp(C’BD).
Lời giải chi tiết
a) Theo giả thiết, ta có:
\({{AM} \over {MD}} = {{D'N} \over {NC'}}\)
\( \Rightarrow {{AM} \over {D'N}} = {{MD} \over {NC'}} = {{AD} \over {D'C'}}\)
Theo định lí Ta-lét đảo ta có MN, AD’, DC’cùng song song với một mặt phẳng (P). Mặt phẳng (P) song song với AD’ và DC’. Nhưng AD’ // BC’ nên mặt phẳng (P) song song với mp(C’BD). Từ đó, ta có MN // (C’BD)
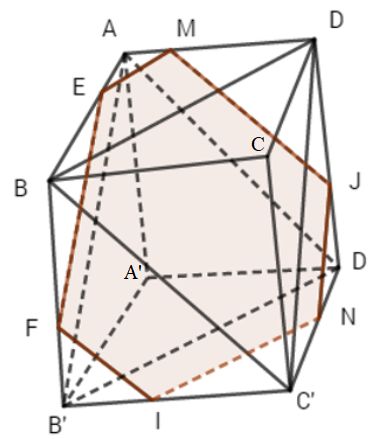
b) Từ M kẻ ME // BD, cắt AB tại E; từ E kẻ đường thẳng EF //AB’, cắt BB’ tại F, từ F kẻ đường thẳng FI // BC’, cắt BC’ tại I; từ N kẻ đường thẳng NJ // C’D cắt D’D tại J. Dễ thấy thiết diện là lục giác MEFINJ có các cạnh đối lần lượt song song với ba cạnh của tam giác C’BD.

