Đề bài
Cho hình chữ nhật ABCD với tâm O, AB = a, BC = 2a. Lấy điểm S trong không gian sao cho SO vuông góc với mặt phẳng (ABCD), đặt SO = h. Gọi M và N lần lượt là trung điểm của AB và CD.
a) Tính góc giữa mp(SMN) với các mặt phẳng (SAB) và (SCD). Tìm hệ thức liên hệ giữa h và a để mp(SMN) vuông góc với các mặt phẳng (SAB), (SCD).
b) Tính góc giữa hai mặt phẳng (SAB) và (SCD). Tính h theo a để hai mặt phẳng đó vuông góc.
Lời giải chi tiết
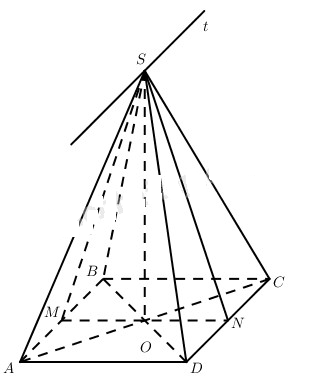
a) Vì \(MN \bot AB,SO \bot AB\) nên \(AB \bot \left( {SMN} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SMN} \right)\). Vậy góc giữa (SMN) và (SAB) cũng bằng 90°.
Tương tự, góc giữa (SMN) và (SCD) cũng bằng 90°.
Như vậy với AB = a, BC = 2a, h tùy ý thì (SMN) vuông góc cả với hai mặt phẳng (SAB) và (SCD).
b) Dễ thấy \(\left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) = St,St//AB\).
Như vậy \(St \bot \left( {SMN} \right)\), từ đó \(\widehat {M{\rm{S}}N}\) hoặc \({180^0} - \widehat {M{\rm{S}}N}\) là góc giữa hai mặt phẳng (SAB) và (SCD).
Tính \(\widehat {M{\rm{S}}N}\).
Ta có
\(S{M^2} = S{N^2} = {h^2} + {a^2} \)
\(M{N^2} = S{M^2} + S{N^2} - 2{\rm{S}}M.SN\cos \widehat {MSN} \)
\(\Leftrightarrow 4{a^2} = {h^2} + {a^2} + {h^2} + {a^2} - 2\left( {{h^2} + {a^2}} \right)\cos \widehat {MSN} \)
tức là \(\cos \widehat {MSN} = {{2{h^2} - 2{a^2}} \over {2\left( {{h^2} + {a^2}} \right)}} = {{{h^2} - {a^2}} \over {{h^2} + {a^2}}}.\)
Vậy góc giữa hai mặt phẳng (SAB) và (SCD) là α mà \(\cos \alpha = \left| {{{{h^2} - {a^2}} \over {{h^2} + {a^2}}}} \right|\).
Từ đó hai mặt phẳng (SAB) và (SCD) vuông góc khi và chỉ khi h = a.
