Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) bất kì không đi qua S, cắt các cạnh bên SA, SB, SC, SD lần lượt tại các điểm A1,B1,C1,D1 . Dùng phương pháp vectơ, chứng minh rằng
SASA1+SCSC1=SBSB1+SDSD1
Lời giải chi tiết
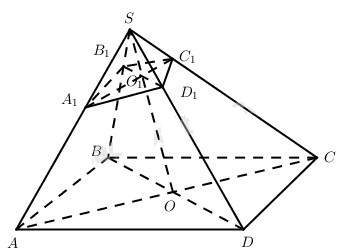
Vì ABCD là hình bình hành nên
→SA+→SC=→SB+→SD
hay →SD=→SA+→SC−→SB
Đặt
→SA=a→SA1,→SB=b→SB1,→SC=c→SC1,→SD=d→SD1
(với a, b, c, d là các số lớn hơn 1)
Khi đó:
SASA1+SCSC1=a+cSBSB1+SDSD1=b+d
và
→SD1=1d.→SD=1d(→SA+→SC−→SB)=1d(a→SA1+c→SC1−b→SB1)=ad.→SA1+cd.→SC1−bd.→SB1
Mặt khác các điểm A1,B1,C1,D1 thuộc mặt phẳng, nên từ đẳng thức đó suy ra
ad+cd−bd=1
tức là a + c = b + d
Như vậy SASA1+SCSC1=SBSB1+SDSD1.

