Lựa chọn câu để xem lời giải nhanh hơn
Cho hai tam giác ABC và A’B’C’ với đường cao lần lượt là AH và A’H’. Trong mỗi trường hợp dưới đây, hai tam giác đó có bằng nhau hay không?
LG a
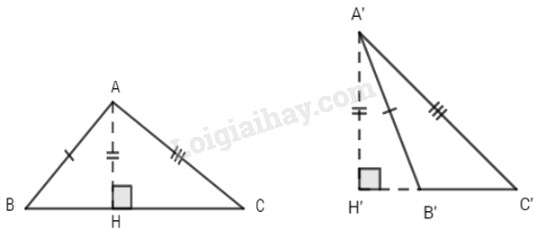
AH = A’H’, AB = A’B’, AC = A’C’;
Lời giải chi tiết:
Có thể không bằng nhau
LG b
AH = A’H’, AB = A’B’, AC = A’C’, các góc A và A’ đều là góc tù.
Lời giải chi tiết:
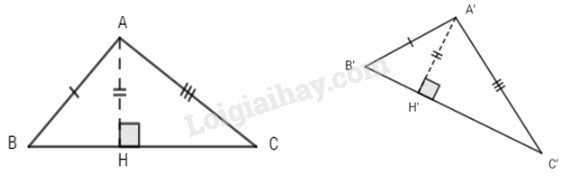
Vì góc \(\widehat A\) và \(\widehat {A'}\) là góc tù nên các góc \(\widehat B,\widehat C,\widehat {B'},\widehat {C'}\) đều là góc nhọn.
Suy ra H ở giữa B và C, H' ở giữa B' và C'.
Vì hai tam giác vuông ABH và A'B'H' bằng nhau nên có phép dời hình F biến A, B, H lần lượt thành A', B', H'.
Dễ thấy rằng khi đó F biến C thành C'.
Vậy F biến tam giác ABC thành tam giác A'B'C' nên hai tam giác đó bằng nhau.
