Đề bài
Chứng minh rằng tiếp tuyến tại điểm bất kì của đồ thị hàm số
\(y = {1 \over 2}\sqrt {x - 4{x^2}} \,\,\,\,(C)\)
Cắt trục tung tại một điểm cách đều tiếp điểm và gốc tọa độ.
Lời giải chi tiết
Để hàm số có đạo hàm thì ta phải có
\(x - 4{x^2} > 0 \Leftrightarrow 0 < x < {1 \over 4}.\)
Với điều kiện \(0 < x < {1 \over 4},\) ta có
\(y' = {{1 - 8x} \over {4\sqrt {x - 4{x^2}} }}.\)
Gọi \({M_0}\left( {{x_0};{y_0}} \right)\) là một điểm tuy ý thuộc đồ thị(C) ; ta có \({y_0} = {1 \over 2}\sqrt {{x_0} - 4x_0^2,} \) \(y' = {{1 - 8{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }}\). Vậy phương trình tiếp tuyến tại \({M_0}\left( {{x_0},{y_0}} \right)\) là
\(y = {{1 - 8{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }}\left( {x - {x_0}} \right) + {1 \over 2}\sqrt {{x_0} - 4x_0^2} \)
Tiếp tuyến này cắt trục tung tại điểm T có tung độ là
\(\eqalign{& {y_T} = {{1 - 8{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }}\left( {0 - {x_0}} \right) + {1 \over 2}\sqrt {{x_0} - 4x_0^2} \cr& \,\,\,\,\, = {{\left( {1 - 8{x_0}} \right)\left( { - {x_0}} \right) + 2\left( {{x_0} - 4x_0^2} \right)} \over {\sqrt {{x_0} - 4x_0^2} }} \cr& = {{{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }} > 0 \cr} \)
Khoảng cách \(T{M_0}\) được tính bởi công thức
\(\eqalign{ T{M_0} &= {\left( {{x_0} - 0} \right)^2} \cr& + {\left( {{1 \over 2}\sqrt {{x_0} - 4x_0^2} - {{{x_0}} \over {\sqrt {{x_0} - 4x_0^2} }}} \right)^2} \cr& = x_0^2{\left( {{{2\left( {{x_0} - 4x_0^2} \right) - {x_0}} \over {\sqrt {{x_0} - 4x_0^2} }}} \right)^2} \cr& = x_0^2 + {{{{\left( {{x_0} - 8x_0^2} \right)}^2}} \over {16\left( {{x_0} - 4x_0^2} \right)}} \cr& = {{16x_0^3 - 64x_0^4 + x_0^2 - 16x_0^3 + 64x_0^4} \over {16\left( {{x_0} - 4x_0^2} \right)}} \cr& = {{x_0^2} \over {16\left( {{x_0} - 4x_0^2} \right)}} \cr} \)
Vậy
\(\left| {T{M_0}} \right| = {{{x_0}} \over {4\sqrt {{x_0} - 4x_0^2} }} = \left| {TO} \right| = {y_T}\)
Điều này chứng tỏ, điểm T cách đều tiếp điểm \({M_0}\) và gốc tọa độ O.
Chú ý: Có thể chứng minh bào toán này bằng phương pháp hình học như sau:
Với \(0 \le x{1 \over 4}\) thì \(y \ge 0\) ta có
\(\eqalign{& y = {1 \over 2}\sqrt {x - 4{x^2}} \Leftrightarrow 4{y^2} + 4{x^2} - x = 0 \cr& \Leftrightarrow {x^2} + {x \over 4} + {y^2} = 0 \cr& \Leftrightarrow {\left( {x - {1 \over 8}} \right)^2} + {y^2} = {\left( {{1 \over 8}} \right)^2} \cr} \)
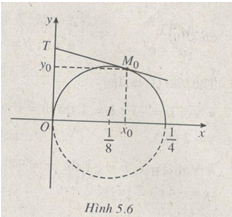
Vậy đồ thị (C) là phần đường tròn thuộc góc phần tư thứ nhất (vì \(x \ge 0\) và \(y \ge 0\)) tâm \(I\left( {{1 \over 8};0} \right)\), bán kính \(R = {1 \over 8}\) (h.5.6)
Áp dụng tính chất: từ một điểm T ngoài đường tròn, kẻ được hai tiếp tuyến với đường tròn là \(TM_0\) và TO và ta có \(|TM_0|=|TO|\) (đpcm).