Đề bài
Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
a) Tìm giao điểm của đường thẳng CD với mp (MNP)
b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ABD).
Lời giải chi tiết
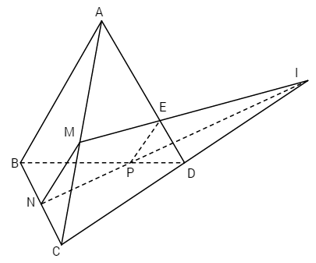
a) Xét mp(BCD), ta có \({{BN} \over {BC}} \ne {{BP} \over {BD}}.\) Suy ra đường thẳng NP cắt đường thẳng CD tại một điểm I. Điểm I thuộc CD và cũng thuộc mp(MNP) nên I chính là giao điểm của CD và mp(NMP).
b) Gọi E là giao điểm của đường thẳng MI và AD. Khi đó, rõ ràng E và P là hai điểm chung của hai mặt phẳng (MNP) và (ABD).
Vậy \(\left( {MNP} \right) \cap \left( {ABD} \right) = EP.\)
