Đề bài
Cho hình lăng trụ ABC. A’B’C’. Gọi I và J lần lượt là trung điểm của BB’ và A’C’. Điểm K thuộc B’C’ sao cho →KC′=−2→KB′ . Chứng minh rằng bốn điểm A, I, J, K cùng thuộc một mặt phẳng.
Lời giải chi tiết
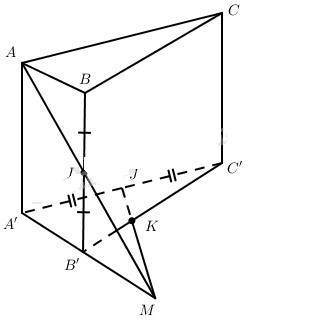
Đặt →AA′=→a,→AB=→b,→AC=→c.
Ta có:
→AI=12(→AB+→AB′)=12(→b+→a+→b)=12(→a+2→b);(1)→AJ=12(→AA′+→AC′)=12(→a+→a+→c)=12(2→a+→c).(2)→AK=→AC′+2→AB′3=→a+→c+2(→a+→b)3=3→a+2→b+→c3.(3)
Từ (1), (2), (3) ta có →AK=23(→AI+→AJ)
Vậy →AI,→AJ,→AK đồng phẳng, tức là các điểm A, I, J, K cùng thuộc một mặt phẳng.
Chú ý: Có thể chứng minh các điểm A, I, J, K thuộc một mặt phẳng bằng cách chứng minh AI và JK cắt nhau tại điểm M.

