Đề bài
Đáy của hình chóp A.BCD là tam giác đều. Đường cao của hình chóp kẻ từ đỉnh A đi qua trung điểm H của cạnh CD. Cắt hình chóp đó bởi mặt phẳng song song với AB và CD và cách đỉnh B một khoảng bằng d. Tính diện tích thiết diện thu được, biết cạnh của tam giác đều BCD là a và AB=a√2.
Lời giải chi tiết
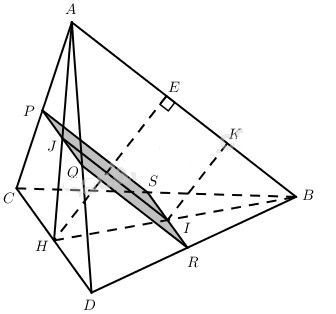
Dễ thấy thiết diện là hình bình hành PQRS. Mặt khác theo giả thiết CD⊥(AHB) nên CD⊥AB. Vậy PQRS là hình chữ nhật.
Kẻ HE⊥AB thì HE⊥(PQRS). Kẻ IK // HE thì IK⊥(PQRS). Do AB // (PQRS) và d(B;(PQRS))=d nên IK = d.
Ta có
HE=AH.HBAB=√AB2−BH2.HBAB=a√154√2
Lại có
IKHE=BIBH=RSCD⇒RS=daa√15.4√2=4√2d√15;BI=IK.BHHE=d.a√32a√154√2=2√2d√5
Mặt khác IJAB=HIHB=(HB−IB)HB;
Từ đó IJ=AB(HB−IB)HB=√2(a√15−4√2d)√15
Vậy SPQRS=RS.IJ=815d(a√15−4√2d) .

