Đề bài
Cho lăng trụ tam giác ABC.A’B’C’. Gọi I, J, K lần lượt là tâm của các hình bình hành ACC’A’, BCC’B’, ABB’A’.
a) Chứng minh rằng: IJ // (ABB’A’), JK // (ACC’A’), IK // (BCC'B’).
b) Ba đường thẳng AJ, CK, BI đồng quy tại một điểm O.
c) Mặt phẳng (IJK) song song với mặt đáy của hình lăng trụ.
d) Gọi G, G’ lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Chứng minh rằng ba điểm G, O, G’ thẳng hàng.
Lời giải chi tiết
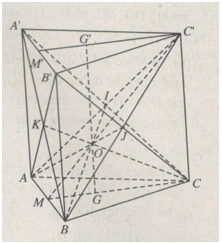
(h.107)
a) Ta có IJ là đường trung bình của tam giác C’AB, nên IJ // AB. Mà AB nằm trên mp(ABB’A’). Vậy IJ // (ABB’A’).
Chứng minh tương tự, ta có:
JK // (ACC’A’), IK // (BCC’B’)
b) Xét ba mặt phẳng (C’AB), (A’BC), (B’AC). Ta có:
\(\eqalign{
& \left( {C'AB} \right) \cap \left( {A'BC} \right) = BI \cr
& \left( {C'AB} \right) \cap \left( {B'AC} \right) = {\rm{AJ}} \cr
& \left( {B'AC} \right) \cap \left( {A'BC} \right) = CK \cr} \)
Vậy theo định lí giao tuyến của ba mặt phẳng thì ba đường thẳng BI, AJ, CK đồng quy tại một điểm.
c) Theo câu a), ta có
\(\left. \matrix{
{\rm{IJ}}//AB \hfill \cr
JK//AC \hfill \cr} \right\} \Rightarrow \left( {{\rm{IJ}}K} \right)//\left( {ABC} \right)\)
d) Dễ thấy O là trọng tâm tam giác C’AB. Gọi M là giao điểm của C’O với AB thì M là trung điểm của AB. Vậy ba điểm M, G, C thẳng hàng.
Vì O và G lần lượt là trọng tâm của hai tam giác C’AB và CAB nên ta có:
\({{MO} \over {MC'}} = {{MG} \over {MC}} = {1 \over 3} \Rightarrow OG//CC'\,\,(1)\)
Chứng minh tương tự OG’ // CC’ (2)
Từ (1) và (2) suy ra ba điểm O, G, G’ thẳng hàng.

