Đề bài
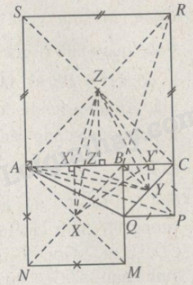
Trên hình 1 có ba điểm thẳng hàng A, B, C và ba hình vuông ABMN, BCPQ, ACRS với tâm lần lượt là X, Y, Z. Gọi X, Y, Z lần lượt là trung điểm của các đoạn thẳng AB, BC, AC.
a) Chứng minh rằng các tam giác Z’XY, X'YZ, Y’XZ là những tam giác vuông cân.
b) Chứng minh rằng hai đoạn thẳng AY, XZ bằng nhau và vuông góc với nhau, cũng như thế đối với hai đoạn BZ, XY và CX, YZ.

Lời giải chi tiết
a) Phép quay tâm B góc quay \({90^o}\) biến A thành M và Q thành C.
Bởi vậy, biến đoạn thẳng AQ thành MC. Suy ra hai đoạn thẳng AQ, MC bằng nhau và vuông góc với nhau.
Chú ý rằng Z’X là đường trung bình của tam giác AMC, còn Z’Y là đường trung bình của tam giác CAQ nên tam giác Z’XY vuông cân tại đỉnh Z’.
Dùng phép quay tâm C góc quay \({90^o}\) ta chứng minh được đoạn thẳng PA, BR bằng nhau và vuông góc với nhau. Suy ra X’YZ là tam giác vuông cân tại X’.
Tương tự cũng chứng minh được Y’XZ là tam giác vuông cân tại Y’.
b) Phép quay tâm X’ góc quay \({90^o}\) biến điểm A thành điểm X và biến Y thành điểm Z.
Suy ra hai đoạn thẳng AY, XZ bằng nhau và vuông góc với nhau.

